| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6, 2001 |
ВЛИЯНИЕ ИМПЕДАНСНЫХ СВОЙСТВ ПОВЕРХНОСТИ
НА ХАРАКТЕРИСТИКИ РАССЕЯНИЯ КРУГОВОГО ЦИЛИНДРА
М.
Ю. Звездина, С. Н. Марченко
Ростовский военный институт ракетных войск
Получена 18 апреля 2001 г.
Приведены соотношения для вычисления компонентов погонной матрицы ЭПР цели бесконечного кругового цилиндра с ненулевым поверхностным импедансом. Коэффициенты матрицы рассеяния получены с использованием импедансных граничных условий. Приведены результаты исследований влияния поверхностного импеданса на характеристики рассеяния кругового цилиндра.
Вопросы проектирования и оценки эффективности функционирования современных радиолокационных систем требуют знания характеристик рассеяния исследуемых объектов. В связи с этим наблюдаемая тенденция применения покрытий с импедансными свойствами для снижения радиолокационной заметности объектов делает актуальной предлагаемую тему исследований. Как показывает анализ работ [1-5], наиболее эффективным способом получения количественных оценок полей рассеяния радиоволн на этапе проектирования является моделирование электромагнитного взаимодействия радиоволн с исследуемым объектом на основе строгой электродинамической модели. Многие радиолокационные объекты имеют форму кругового цилиндра. Однако известные в настоящее время модели рассеяния электромагнитной волны на таких поверхностях [6-11] рассматривают частные случаи значений поверхностного импеданса.
Целью статьи является создание модели рассеяния электромагнитных полей на анизотропном импедансном круговом цилиндре и проведение исследований влияния параметров импеданса на характеристики рассеяния.
В
качестве основной энергетической характеристики рассеяния будем рассматривать
эффективную площадь рассеяния (ЭПР)
![]() цели. Как показано в [5], влиянием торцов
цилиндра радиуса a можно пренебречь, если его длина L
удовлетворяет условию
цели. Как показано в [5], влиянием торцов
цилиндра радиуса a можно пренебречь, если его длина L
удовлетворяет условию
![]() (
(![]() ‑ длина волны передатчика).
‑ длина волны передатчика).
Для протяженных объектов, к которым можно отнести бесконечный круговой цилиндр, при вычислении погонной ЭПР необходимо соблюдать два условия [5]: падающая волна в месте расположения объекта должна быть плоской (монохроматической) и амплитуда отраженной волны должна измеряться на бесконечно большом удалении от рассеивающего объекта.
Применительно к дифракционным задачам предельно допустимое расстояние до объекта, при котором можно не учитывать сферичность волны, т.е. дальняя зона, в зависимости от требуемой точности вычислений определяется условием [1, 2, 5]
где
b=1,…,4;
![]() ‑ наибольший поперечный к
направлению распространения волны размер объекта.
‑ наибольший поперечный к
направлению распространения волны размер объекта.
Поскольку электромагнитные волны обладают определенной поляризацией излучения, а объект может выполнять преобразование поляризации на частоте падающего поля, то матрица погонной ЭПР в поляризационном линейно ортогональном базисе в квазистационарном приближении определяется соотношением [12]
В
выражении (2) множитель
![]() , описывающий временную зависимость,
опущен; индексы элементов матрицы
, описывающий временную зависимость,
опущен; индексы элементов матрицы
![]() идентифицируют поляризационный способ
локации объектов; а
идентифицируют поляризационный способ
локации объектов; а
![]() -элемент матрицы (
-элемент матрицы (![]() ) описывается выражением
[8]
) описывается выражением
[8]
где
![]() ‑
‑
![]() -компонента
рассеянного поля в точке приема
-компонента
рассеянного поля в точке приема
![]() при возбуждении
при возбуждении
![]() -компоненты поля
-компоненты поля
![]() в точке
источника
в точке
источника
![]() .
.
Поляризационный
базис путем несложных преобразований координат всегда может быть выбран таким
образом, чтобы при построении систем координат источника и приемника ориентации
базисов удовлетворяли векторному уравнению локально-плоской волны [1,
2], а
падающее и рассеянное поля имели горизонтальную и вертикальную составляющие. В
цилиндрической системе координат, в которой ищется решение дифракционной задачи
для кругового цилиндра, горизонтальная составляющая поля соответствует
![]() -компоненте
поля, а вертикальная ‑
-компоненте
поля, а вертикальная ‑
![]() - или z-компоненте.
- или z-компоненте.
Для представления составляющих поля воспользуемся результатами работ [13, 14], а также асимптотиками цилиндрических функций для больших значений аргументов [15]. Вертикальная и горизонтальная составляющие падающего поля при этом определяются соотношениями
где
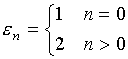 ‑
числа Неймана;
‑
числа Неймана;
![]() Ом;
Ом;
![]() ;
;
![]() ;
;
![]() ‑ амплитуда волны
источника.
‑ амплитуда волны
источника.
Рассеянное поле для ортогональных компонентов отраженной волны описывается формулами
где
![]() ‑
матрица рассеяния, коэффициенты которой для кругового цилиндра с анизотропным
поверхностным импедансом на основании работ [13, 14] могут быть записаны в виде
‑
матрица рассеяния, коэффициенты которой для кругового цилиндра с анизотропным
поверхностным импедансом на основании работ [13, 14] могут быть записаны в виде
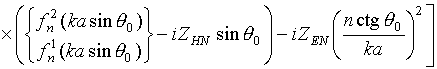 ;
;
где
![]() ‑
функция Бесселя n-го порядка и ее производная;
‑
функция Бесселя n-го порядка и ее производная;
![]() ‑ функция
Ганкеля 2-го рода n-го порядка и ее производная;
‑ функция
Ганкеля 2-го рода n-го порядка и ее производная;
![]() ;
;
![]() ;
;
![]() ‑ компоненты
тензора поверхностного импеданса.
‑ компоненты
тензора поверхностного импеданса.
Поскольку поверхностные волны, возбуждаемые при дифракции плоской волны на импедансной поверхности кругового цилиндра, не распространяются в радиальном направлении, то в дальней зоне их вклад в рассеянное поле практически равен нулю [16].
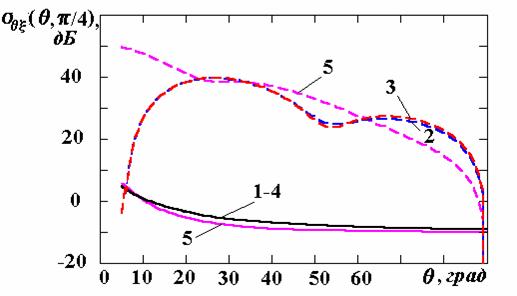
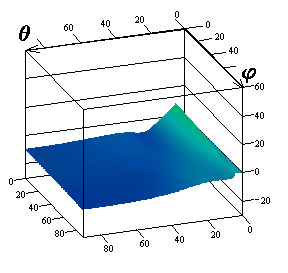
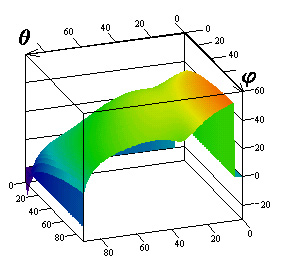
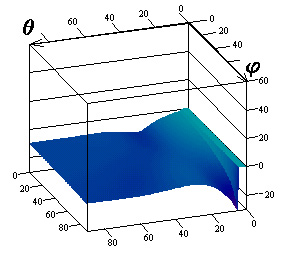
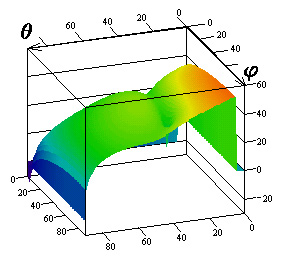
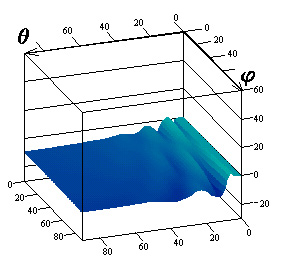
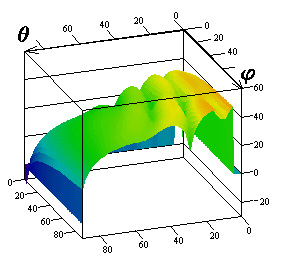
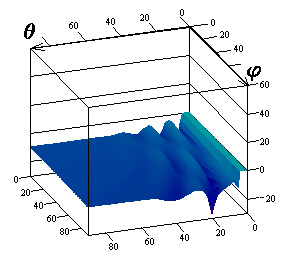
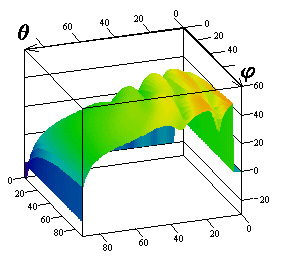
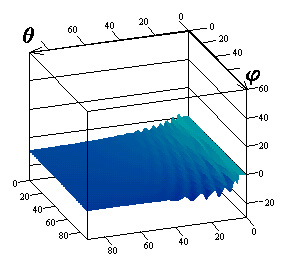
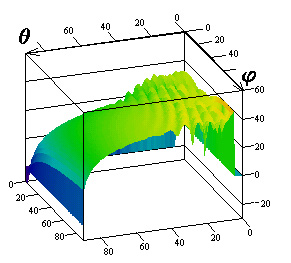
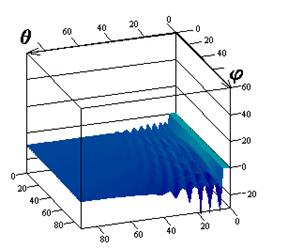
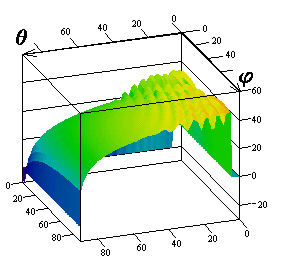
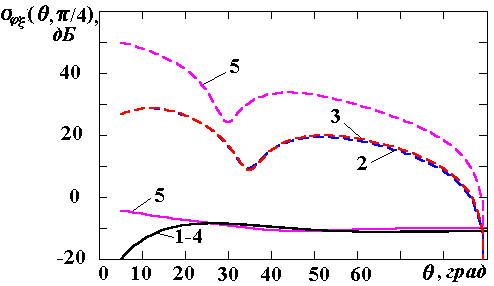
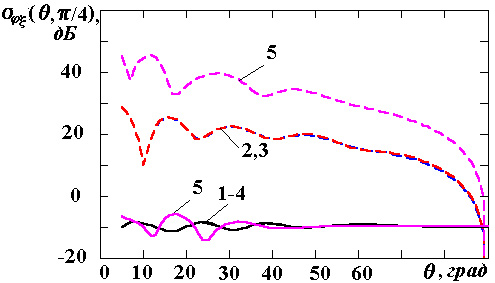
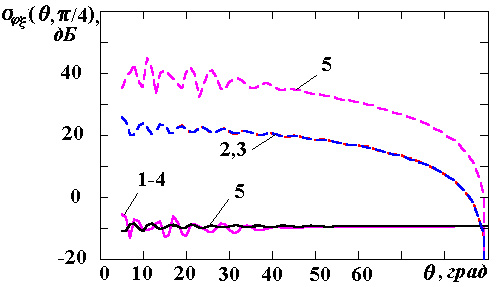
Результаты
исследований влияния параметров поверхностного импеданса на элементы матрицы
погонной двухпозиционной ЭПР кругового цилиндра для радиусов
![]() приведены на
рис.1-3 соответственно. Рисунки с индексами "а", "в",
"г" соответствуют случаю вертикальной поляризации падающей волны, с
индексами "б", "д", "е" ‑ горизонтальной.
Причем поля рисунков с индексами "а", "б" иллюстрируют
сечения
приведены на
рис.1-3 соответственно. Рисунки с индексами "а", "в",
"г" соответствуют случаю вертикальной поляризации падающей волны, с
индексами "б", "д", "е" ‑ горизонтальной.
Причем поля рисунков с индексами "а", "б" иллюстрируют
сечения
![]() объемных
компонентов матрицы ЭПР (
объемных
компонентов матрицы ЭПР (![]() и
и
![]() соответственно), а с индексами
"в"-"е" ‑ сами компоненты матрицы ЭПР:
соответственно), а с индексами
"в"-"е" ‑ сами компоненты матрицы ЭПР:
![]() ,
,
![]() ,
,
![]() ,
,
![]() . В качестве
характеристического размера рассеивателя использовался диаметр кругового
цилиндра. Сплошными линиями на рисунках с индексами "а",
"б" показаны сечения основных элементов матрицы ЭПР цели,
соответствующие прямым преобразованиям компонентоов падающей волны; штриховыми
линиями ‑ соответствующие сечения деполяризационных элементов матрицы,
описывающих перекрестные преобразования.
. В качестве
характеристического размера рассеивателя использовался диаметр кругового
цилиндра. Сплошными линиями на рисунках с индексами "а",
"б" показаны сечения основных элементов матрицы ЭПР цели,
соответствующие прямым преобразованиям компонентоов падающей волны; штриховыми
линиями ‑ соответствующие сечения деполяризационных элементов матрицы,
описывающих перекрестные преобразования.
Как
известно, импедансные свойства поверхности, характеризуемые тензором
поверхностного импеданса, могут быть реализованы различными способами,
например, нанесением тонкого слоя магнитодиэлектрика на металлическую
поверхность (изотропный импеданс,
![]() ), гребенчатыми структурами (анизотропный
импеданс), канавки которых ориентированы либо перпендикулярно образующей цилиндра
(
), гребенчатыми структурами (анизотропный
импеданс), канавки которых ориентированы либо перпендикулярно образующей цилиндра
(![]() ,
,
![]() ) либо
параллельно образующей цилиндра (
) либо
параллельно образующей цилиндра (![]() ,
,
![]() ) и т.д. В связи с этим исследования
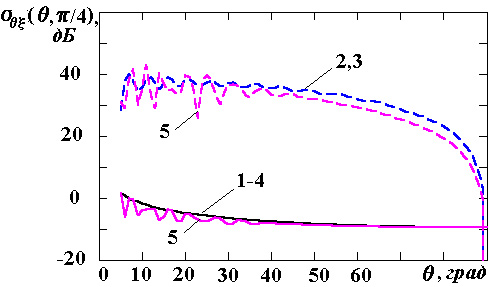
проводились для различных способов реализации поверхностного импеданса. Так, на
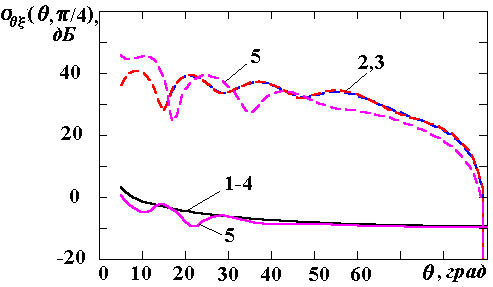
рисунках с индексами "а", "б" кривыми 1-5 показаны результаты,
полученные для следующих значений тензора поверхностного импеданса: идеально
проводящей поверхности (
) и т.д. В связи с этим исследования
проводились для различных способов реализации поверхностного импеданса. Так, на
рисунках с индексами "а", "б" кривыми 1-5 показаны результаты,
полученные для следующих значений тензора поверхностного импеданса: идеально
проводящей поверхности (![]() , кривые 1); изотропного импеданса (кривые
2); и двух вариантов анизотропного импеданса (
, кривые 1); изотропного импеданса (кривые
2); и двух вариантов анизотропного импеданса (![]() ,
,
![]() ‑ кривые 3 и
‑ кривые 3 и
![]() ,
,
![]() ‑ кривые
4 соответственно). Величина поверхностного импеданса кривых 2-4
‑ кривые
4 соответственно). Величина поверхностного импеданса кривых 2-4
![]() выбрана на
основании данных из работы [8]. Кривые с номером 5, а также рисунки с индексами
"в" - "е" иллюстрируют поведение основной и
деполяризационной компонент матрицы ЭПР для случая изотропного поверхностного
импеданса с величиной
выбрана на
основании данных из работы [8]. Кривые с номером 5, а также рисунки с индексами
"в" - "е" иллюстрируют поведение основной и
деполяризационной компонент матрицы ЭПР для случая изотропного поверхностного
импеданса с величиной
![]() [7]. Исключение области осевого облучения
объекта при проведении исследований связано со сделанным ранее предположением о
пренебрежении влиянием торцов цилиндра на величину рассеянного поля.
[7]. Исключение области осевого облучения
объекта при проведении исследований связано со сделанным ранее предположением о
пренебрежении влиянием торцов цилиндра на величину рассеянного поля.
Анализ
полученных результатов показывает, что характеристики рассеяния, найденные при
использовании импедансных граничных условий (рис.1,а), с достаточной точностью
совпадают с аналогичными параметрами, полученными в [8] методом сшивания полей
при решении задачи дифракции. Нанесение покрытий с ненулевым поверхностным
импедансом изменяет структуру отраженного поля. Поскольку падающее и рассеянное
поля имеют различную угловую зависимость, то перекрестные компоненты матрицы ЭПР цели появляются в секторе углов, отличающемся от направления облучения
объекта. При этом для ряда значений поверхностного импеданса, например,
изотропного и анизотропного с
![]() , перекрестные компоненты матрицы ЭПР
значительно превышают основные компоненты. Особенно ярко данное явление
наблюдается при облучении объекта в продольном направлении и волнами с
горизонтальной поляризацией.
, перекрестные компоненты матрицы ЭПР
значительно превышают основные компоненты. Особенно ярко данное явление
наблюдается при облучении объекта в продольном направлении и волнами с
горизонтальной поляризацией.
Несложно
заметить, что применение покрытий с анизотропными свойствами является более
перспективным направлением по сравнению с покрытиями с изотропными свойствами.
Данные структуры позволяют для ряда случаев получать требуемые характеристики
рассеяния без увеличения уровня деполяризационных компонентов матрицы рассеяния
цели. Так, для гребенчатых структур, образованных канавками, параллельными
образующей цилиндра (![]() ), позволяют сформировать такое отраженное
поле, в котором отсутствовали бы перекрестные компоненты.
), позволяют сформировать такое отраженное
поле, в котором отсутствовали бы перекрестные компоненты.
Увеличение радиуса кругового цилиндра, а также величины реактанса поверхности приводит к тому, что компоненты ЭПР приобретают в угломестных направлениях осциллирующий характер, обусловленный интерференцией полей когерентных виртуальных источников [5], формируемых на поверхности рассеивающего объекта полем падающей волны. Следовательно, соответствующим подбором значения поверхностного реактанса можно для ряда направлений добиться уменьшения и основных компонентов матрицы ЭПР.
Таким образом, предложенная модель рассеяния электромагнитных полей на анизотропном круговом цилиндре позволяет с достаточной для практических целей точностью получать характеристики рассеяния протяженного объекта. Проведенные с ее использованием исследования влияния величины поверхностного импеданса на матрицу ЭПР цели показали, применение покрытий с ненулевым поверхностным импедансом изменяет структуру отраженного от объекта поля. Величина перекрестных компонентов матрицы ЭПР зависит как от величины и типа импеданса, так и поляризации падающего поля. Для снижения уровня перекрестных компонентов целесообразно применение покрытий, реализующих анизотропный импеданс, эквивалентный импедансу, реализуемому гребенчатой структурой с канавками, параллельными образующей цилиндра. Соответствующим подбором величины реактанса можно для ряда направлений уменьшить и уровень основных компонентов ЭПР.
а
б
|
в |
г |
|
д |
е |
Рис.1. Компоненты матрицы ЭПР для радиуса цилиндра
![]()
а
б
|
в |
г |
|
д |
е |
Рис.2. Компоненты матрицы ЭПР для радиуса цилиндра
![]()
а
б
|
в |
г |
|
д |
е |
Рис.3. Компоненты матрицы ЭПР для радиуса цилиндра
![]()
Литература
1. Антифеев В.Н., Борзов А.Б., Быстров Р.П., Исаев И.Ш., Соколов А.В. Математические модели рассеяния электромагнитных волн на объектах сложной формы // Зарубежная радиоэлектроника. Успехи радиоэлектроники. 1998. №10. С.39-54.
2. Борзов А.Б., Быстров Р.П., Соколов А.В. Анализ радиолокационных характеристик объектов сложной пространственной конфигурации // "Журнал радиоэлектроники". 1998. №1. http://jre.cplire.ru/win/dec98/4/text.html
3. Ковалев С.В., Нестеров С.М., Скородумов И.И. Расчет радиолокационных характеристик объектов с учетом влияния поверхностных волн и щелевых образований // радиотехника и электроника. 1998. Т.43. №1. С.37-46.
4. Еремин Ю.А., Зимнов М.Х., Кюркчан А.Г. Теоретические методы анализа характеристик рассеяния электромагнитных волн. Стационарные задачи // Радиотехника и электроника. 1992. Т.37. №1. С.14-31.
5. Штагер Е.А. Рассеяние радиоволн на телах сложной формы. ‑ М.: Радио и связь, 1986. ‑ 184 с.
6. Graglia R.D., Uslenghi P.L.E., Vitiello R., D'Elia U. Electromagnetic scattering for oblique incidence on impedance bodies of revolution // IEEE Trans. AP-47. 1995. №1ю С.11-26.
7. Климов А.В., Петров Б.М., Семенихин А.И. Рассеяние на цилиндре с анизотропным импедансом // Изв. вуз. Радиоэлектроника. 1985. Т.28. №2. С.74-78.
8. Tenneti C.R. Plane wave scattering by a corrugated conducting cylinder at oblique incidence // IEEE Trans. AP-36. 1988. №8. С.1184-1188.
9. Mosallaei H., Rahmat-Samii Y. RSC reduction of canonical targets using genetic algorithm synthesized RAM// IEEE Trans. AP-48. 2000. №10. С.1594-1607.
10. Соппа М.С., Ершова Е.Е. Численное решение задачи рассеяния на импедансных телах при Е- и Н-поляризациях // Автометрия. 1997. №2. С.56-60.
11. Петров Б.М., Семенихин А.И. Управляемые импедансные покрытия и структуры // Зарубежная радиоэлектроника. 1994. №6. С.9-16.
12. Теоретические основы радиолокации / Под ред. В.Е. Дулевича. ‑ М.: Сов. радио, 1978. ‑ 608 с.
13. Габриэльян Д.Д., Звездина М.Ю. Влияние импедансной поверхности кругового цилиндра на диаграмму направленности электрического диполя // Радиотехника и электроника. 2000. Т.45. №10. С.1194-1197.
14. Габриэльян Д.Д., Звездина М.Ю., Костенко П.И. Влияние импедансной поверхности цилиндра на характеристики излучения // "Журнал радиоэлектроники". 2000. №2. http://jre.cplire.ru/win/feb00/5/text.html
15. Справочник по специальным функциям с формулами, графиками и таблицами / Под. ред М. Абрамовица и И.Стиган. ‑ М.: Наука, 1979. ‑ 832 с
16. Ерохин Г.А., Кочержевский В.Г., Гофман В.Г. Синтез цилиндрических антенных решеток импедансного типа / В сб. Антенны. Вып.17. ‑ М.: Связь, 1973. С.43-52.
Авторы:
Звездина Марина Юрьевна ‑ кандидат технических наук, РВИ РВ, zvezd@jeo.ru
Марченко Сергей Николаевич ‑ курсант РВИ РВ.
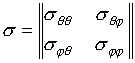 .
(2)
.
(2)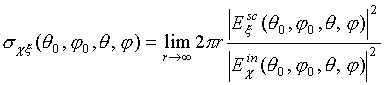 ,
(3)
,
(3)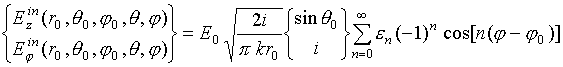 ,
(4)
,
(4)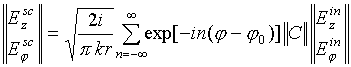 ,
(5)
,
(5)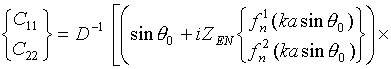 (6)
(6)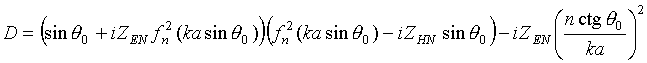 ;
(8)
;
(8)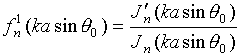 ;
(9)
;
(9)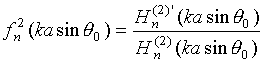 ;
(10)
;
(10)