

Next: Simulation Results
Up: Approximation of distribution function
Previous: The Exact Analytical Expression
The exact analytical expression (12) of the
moments can be also used for the determination of the PDF of
the test-statistic 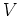 . The PDF
. The PDF 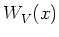 of the random
variable
of the random
variable 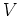 can be represented as a series from a full
system of orthogonal polynomials
can be represented as a series from a full
system of orthogonal polynomials 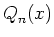
|
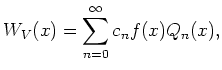
|
|
|
(13) |
where 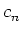 are the coefficients of this expansion and
are the coefficients of this expansion and
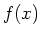 is a given weight function which determines the set
of orthogonal polynomials
is a given weight function which determines the set
of orthogonal polynomials 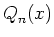 .
.
The basic problem that arises by using the
expansion (13) consists in the choice of the
weight function 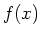 for which this series has the most
rapid convergence rate [5]. For this purpose as
weight function
for which this series has the most
rapid convergence rate [5]. For this purpose as
weight function 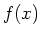 , the beta density function was chosen
, the beta density function was chosen
|
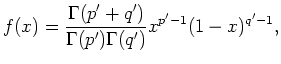
|
|
|
(14) |
|
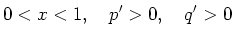
|
|
|
(15) |
The investigation carried out has shown that the
function (14) is a very successful zero
approximation of the analytically unknown PDF of the
test-statistic 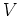 . For this weight function, the set of
orthogonal polynomials
. For this weight function, the set of
orthogonal polynomials 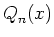 is a system of biased
orthogonal Jacobi polynomials defined on the interval [0,1].
These polynomials are written as follows
is a system of biased
orthogonal Jacobi polynomials defined on the interval [0,1].
These polynomials are written as follows
|
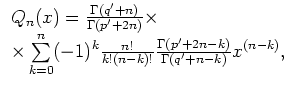
|
|
|
(16) |
From the condition of equalities for the first two moments
of the beta probability distribution (14) and the
test-statistic 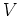 (12) it is possible to
evaluate two parameters
(12) it is possible to
evaluate two parameters 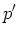 and
and 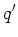 which do not depend
upon the beta density function
which do not depend
upon the beta density function 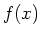 . Therefore, the
moments of the beta distribution are equal to
. Therefore, the
moments of the beta distribution are equal to
|
![$\displaystyle M[\beta^k]=\frac{\Gamma(p'+q')\Gamma(p'+k)}{\Gamma(p')\Gamma(p'+q'+k)},$](img80.png)
|
|
|
(17) |
From (12) and (17) the system of two equations for the unknown parameters 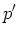 and
and 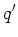 can be obtained
can be obtained
|
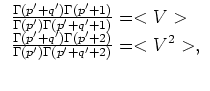
|
|
|
(18) |
that can be simplified to
|
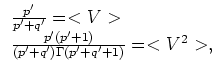
|
|
|
(19) |
Because the parameters 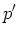 and
and 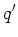 are positive and the
values of all moments
are positive and the
values of all moments ![$M[V^h]$](img83.png) are in the interval [0,1] it
can be easily shown that for any values of the first two
moments of the random variable
are in the interval [0,1] it
can be easily shown that for any values of the first two
moments of the random variable 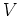 and for any
and for any 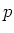 and
and 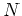 there is unique solution of the system (19)
there is unique solution of the system (19)
|

|
|
|
(20) |
Substituting (20) into
expression (14), we can obtain the zero
approximation for the PDF 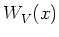 (the first term in the
series expansion (13)). It can be derived that the
following two coefficients in the expansion (13)
are identically equal to zero (
(the first term in the
series expansion (13)). It can be derived that the
following two coefficients in the expansion (13)
are identically equal to zero (
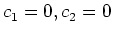 ) for any
) for any
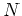 and
and 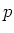 .
.
Higher order coefficients 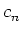 (
(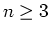 ) in the expansion
can be expressed as function of the known test-statistic
) in the expansion
can be expressed as function of the known test-statistic 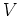 moments (of order
moments (of order 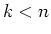 ) by a standard procedure which
involves the condition of mutual orthogonality of the
polynomials
) by a standard procedure which
involves the condition of mutual orthogonality of the
polynomials 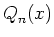 . The common expression for
. The common expression for 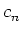 is
given by
is
given by
|
![$\displaystyle \begin{array}{l}
c_n
= \frac{(2n+p)\Gamma^2(2n+p)}{n!\Gamma(n+q)\...
...n}(-1)^k
\frac{n!\Gamma(p+2n-k)} {k!(n-k)!\Gamma(q+n-k)}
M[V^{n-k}]
\end{array}$](img88.png)
|
|
|
(21) |
As it can be seen from the simulation results shown in the
next section, the series (13) with
coefficients (21) has a very high rate of
convergence to 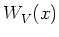 in the whole definition interval
[0,1].
in the whole definition interval
[0,1].



Next: Simulation Results
Up: Approximation of distribution function
Previous: The Exact Analytical Expression
![]() for which this series has the most
rapid convergence rate [5]. For this purpose as
weight function
for which this series has the most
rapid convergence rate [5]. For this purpose as
weight function ![]() , the beta density function was chosen
, the beta density function was chosen
![]() (
(![]() ) in the expansion
can be expressed as function of the known test-statistic
) in the expansion
can be expressed as function of the known test-statistic ![]() moments (of order
moments (of order ![]() ) by a standard procedure which
involves the condition of mutual orthogonality of the
polynomials
) by a standard procedure which
involves the condition of mutual orthogonality of the
polynomials ![]() . The common expression for
. The common expression for ![]() is
given by
is
given by