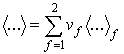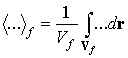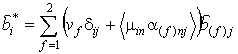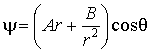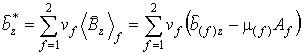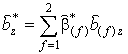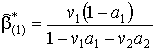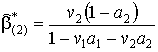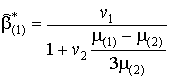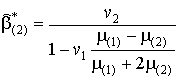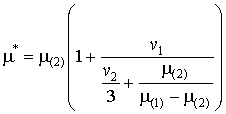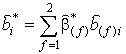УДК 537.8
ЭФФЕКТИВНЫЕ СВОЙСТВА НАМАГНИЧЕННЫХ СТРУКТУР С ПОЛИДИСПЕРСНЫМИ СФЕРИЧЕСКИМИ ВКЛЮЧЕНИЯМИ
А. А. Паньков
Пермский национальный исследовательский политехнический университет
Получена 11 июня 2014 г.
Аннотация. Получены новые решения для эффективных остаточных магнитных индукций различных полидисперсных структур со сферическими зернами неоднородностями с учетом произвольной взаимной ориентации векторов начальных магнитных индукций фаз. Рассмотрены частные случаи: намагниченные включения в эластомере, поры в намагниченной среде и взаимообратная намагниченность фаз. Представлены численные результаты сравнительного анализа зависимостей эффективных остаточных магнитных индукций различных намагниченных полидисперсных структур со сферическими включениями.
Ключевые слова: композит, эффективные свойства, полидисперсная структура.
Abstract. New decisions for effective residual magnetic induction of various polydisperse structures with spherical grains not uniformity taking into account any mutual orientation of vectors of initial magnetic induction of phases are received. Special cases are considered: the magnetized inclusions in an elastomer, a time in the magnetized environment and inverse magnetization of phases. Numerical results of the comparative analysis of dependences of effective residual magnetic induction of various magnetized polydisperse structures with spherical inclusions are presented.
Key words: composite, effective properties, polydisperse structure.
Введение
Магнитные материалы [1] находят широкое применение в современной электротехнике, радиотехнике и автоматике в качестве автономных источников постоянного магнитного поля и магнитоуправляемых материалов, способных изменять свои свойства и деформироваться нужным образом под действием внешних магнитных полей [2‑4]. Создание композитных материалов с намагниченными фазами позволяет получить новые магнитные материалы с заданным и управляемым комплексом физико-механических свойств. Интерес к исследованию полидисперсных моделей обусловлен возможностью получения точных, в рамках модели, аналитических решений для эффективных модулей и структурных полей композитов.
Цель работы – обобщение известных решений [5‑8] для магнитных полей и эффективных проницаемостей полидисперсных структур на случай наличия у фаз начальных намагниченностей.
1. Микро и макро уровни магнитных свойств композита
1.1. Определяющие соотношения
Рассматриваем двухфазные магнитные
среды в представительной микронеоднородной области ![]() . На
структурном или «микроуровне» композита определяющие соотношения
. На
структурном или «микроуровне» композита определяющие соотношения
связывают в каждой точке ![]() поля индукции
поля индукции ![]() и
напряженности
и
напряженности ![]() магнитного поля через
микронеоднородные кусочно-постоянные поля магнитных проницаемостей
магнитного поля через
микронеоднородные кусочно-постоянные поля магнитных проницаемостей
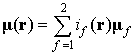
и начальных магнитных индукций
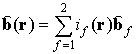 ,
,
где известные для каждой фазы ![]() тензор магнитных проницаемостей
тензор магнитных проницаемостей ![]() и вектор начальной магнитной индукции
и вектор начальной магнитной индукции ![]() , индикаторная функция
, индикаторная функция ![]() -й фазы
-й фазы
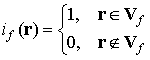
представительная область 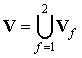 , область фазы
, область фазы ![]() ,
, ![]() .
Относительное объемное содержание
.
Относительное объемное содержание ![]() -й фазы в композите
-й фазы в композите ![]() , операторы осреднения
, операторы осреднения
по представительной области ![]() и по
и по ![]() -й фазе
-й фазе ![]() композита
соответственно.
композита
соответственно.
На макроуровне представительной области ![]() композита определяющие соотношения (1)
композита определяющие соотношения (1)
![]() (3)
(3)
Выражения для определения эффективных
величин ![]() ,
, ![]() получим
осреднением
получим
осреднением ![]() уравнения (1)
уравнения (1)
![]()
в виде
с использованием возможного разложения микроуровневой напряженности магнитного поля
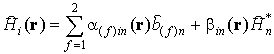
через неизвестные пока тензорные поля
![]() ,
, ![]() по
заданным векторам начальных магнитных индукций
по
заданным векторам начальных магнитных индукций ![]() фаз и
макронапряженности
фаз и
макронапряженности ![]() композита; символы Кронекера
композита; символы Кронекера
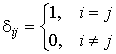
Решения (4) можно выразить
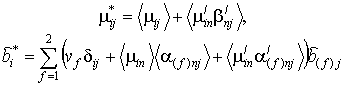 (5)
(5)
через пульсации «![]() » в разложениях
» в разложениях
![]() ,
,
![]() ,
,
![]() ,
,
где осредненные величины
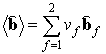 ,
,
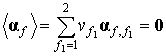 ,…
,…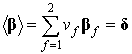
с учетом обозначений: ![]() ,
, ![]() , (2).
, (2).
1.2 Полидисперсные структуры
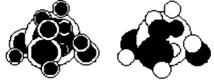
На
рис. 1 приведены фрагменты различных полидисперсных двухфазных структур со
сферическими включениями, черным цветом обозначена 1-я фаза, белым – 2-я фаза.
Распределение частиц: составных двухфазных на рис. 1,а или однофазных на рис.
1,б и сфер по размерам достаточно широко, включая и бесконечно малые. Это
обуславливает возможность заполнения полидисперсными частицами всей
представительной области ![]() композита.
композита.
а б
Рис. 1. Фрагменты полидисперсных структур
Модель структуры на рис. 1,а состоит из однотипных
составных полидисперсных частиц – сфер из 1-й фазы, окруженных сферическими
слоями 2-й фазы композита. Такая структура сохраняет свойство матричности 2-й
фазы при всех возможных степенях наполнения области ![]() 1-й
фазой
1-й
фазой ![]() ,
, ![]() , где
, где ![]() ,
, ![]() ‑
внутренний и наружный радиусы произвольной составной сферической частицы.
‑
внутренний и наружный радиусы произвольной составной сферической частицы.
Модель структуры на рис. 1,б состоит из однородных
полидисперсных частиц двух типов: сфер из 1-й и 2-й фаз композита. Объемные
доли сфер из 1-й фазы ![]() и из 2-й фазы
и из 2-й фазы ![]() . Структура на рис. 1,б инвариантна к
инверсии свойств 1-й и 2-й фаз при фиксированной объемной доле фаз.
. Структура на рис. 1,б инвариантна к
инверсии свойств 1-й и 2-й фаз при фиксированной объемной доле фаз.
Решения для магнитных полей в различных
полидисперсных структурах (рис.1) при ![]() ,
, ![]() получим на основе принципа суперпозиции
через суммы соответствующих решений для случая
получим на основе принципа суперпозиции
через суммы соответствующих решений для случая ![]() ,
, ![]() (известное решение [5]) и случая
(известное решение [5]) и случая ![]() ,
, ![]() для
расчетных схем: одиночное сферическое включение в эффективной среде (для
структуры на рис.1,б), одиночное включение со сферической прослойкой матрицы в
эффективной среде и (или) составная сферическая ячейка (для структуры на
рис.1,а) на основе известных общих решений [5] осесимметричной задачи.
для
расчетных схем: одиночное сферическое включение в эффективной среде (для
структуры на рис.1,б), одиночное включение со сферической прослойкой матрицы в
эффективной среде и (или) составная сферическая ячейка (для структуры на
рис.1,а) на основе известных общих решений [5] осесимметричной задачи.
2. Одноосная ориентация начальных магнитных индукций фаз композита
Рассмотрим случай, когда векторы ![]() начальных магнитных индукций фаз
полидисперсных структур (рис.1) коллинеарны оси
начальных магнитных индукций фаз
полидисперсных структур (рис.1) коллинеарны оси ![]() .
.
2.1 Общие решения осесимметричной задачи
Для случая осевой по ![]() симметрии задачи в сферической система
координат:
симметрии задачи в сферической система
координат: ![]() ,
, ![]() ,
, ![]() имеем для полого шара
имеем для полого шара ![]() общие решения [5]:
общие решения [5]:
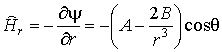 ,
(6)
,
(6)
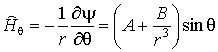 ,
, ![]()
при
этом напряженность по оси ![]()
![]()
и среднее значение по рассматриваемой области полого шара
![]() .
(7)
.
(7)
Для случая изотропной магнитной проницаемости
материала ![]() индукции магнитного поля
индукции магнитного поля
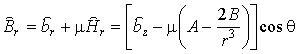 ,
,
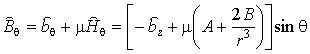 ,
,
![]() ;
;
среднее значение по рассматриваемой области полого шара
с учетом (7).
Далее, для
различных полидисперсных структур (рис.1) будем рассматривать случай ![]() ,
, ![]() .
.
2.2 Сферическое включение в эффективной среде
К такой расчетной
схеме приходим, заменив окружающую неоднородную среду вокруг одиночного
сферического зерна неоднородности (со свойствами 1-й или 2-й фазы) однородной
средой с эффективными свойствами композита. Запишем соответствующие общие
решения (6) для шара со свойствами 1-й фазы композита в неограниченной среде с
искомыми эффективными свойствами композита. Здесь и далее обозначим через ![]() ,
, ![]() константы
интегрирования для соответствующих областей со свойствами
константы
интегрирования для соответствующих областей со свойствами ![]() -й фазы композита;
-й фазы композита; ![]() ,
,
![]() ‑ для области с эффективными
свойствами композита.
‑ для области с эффективными
свойствами композита.
Константы
интегрирования найдем из условий: ограниченности потенциала при ![]() (
(![]() ),
непрерывности магнитного потенциала
),
непрерывности магнитного потенциала ![]() и индукции
и индукции ![]() на границе при
на границе при ![]() и
условия на бесконечности при
и
условия на бесконечности при ![]() :
:
![]() ,
,
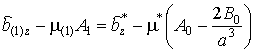 ,
,
![]() ;
;
из последнего уравнения следует
равенство ![]() ; решение для константы
; решение для константы
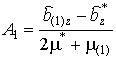 (9)
(9)
Далее рассмотрим вторую задачу об одиночном шаре со свойствами 2-й фазы композита в эффективной среде и получим решение для константы
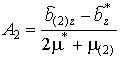 (10)
(10)
аналогично (9).
Для
рассматриваемой модели (рис.1,а) эффективная остаточная макроиндукция ![]() магнитного поля композита рассчитывается
через значения осредненных индукций в одиночных шаровых включениях первой
магнитного поля композита рассчитывается
через значения осредненных индукций в одиночных шаровых включениях первой ![]() и второй
и второй ![]() задач
задач
Выразим ![]() из
(11), учитывая зависимость констант
из
(11), учитывая зависимость констант ![]() ,
, ![]() (9), (10) от величины
(9), (10) от величины ![]() .
.
В результате получим решение для эффективной остаточной магнитной индукции композита
где коэффициенты
с учетом
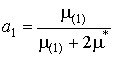 ,
,
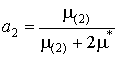
Поиск решения
для эффективной магнитной проницаемости ![]() композита
с рассматриваемой полидисперсной структурой (рис.1,а) представляет собой
отдельную задачу, для которой
композита
с рассматриваемой полидисперсной структурой (рис.1,а) представляет собой
отдельную задачу, для которой ![]() ,
, ![]() . Опуская промежуточные выкладки, запишем
выражение
. Опуская промежуточные выкладки, запишем
выражение
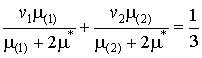
из которого искомая величина ![]() находится как решение
находится как решение
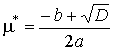
квадратного уравнения
![]() ,
,
где коэффициенты: ![]() ,
, ![]() ,
, ![]() , дискриминант
, дискриминант ![]() ,
среднее значение
,
среднее значение 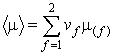 .
.
2.3 Сферическое включение с прослойкой матрицы в эффективной среде
К такой расчетной схеме – «трехфазная модель» [5],
приходим, если заменим неоднородную среду вокруг одиночной составной
сферической ячейки однородной средой с эффективными свойствами композита.
Запишем соответствующие общие решения (6) для каждой из трех областей
рассматриваемой расчетной схемы – шар (1-я фаза, включения композита) со
сферической оболочкой (2-я фаза, матрица композита) в неограниченной среде с
искомыми эффективными свойствами композита. Константы интегрирования найдем из
условий: ограниченности потенциала при ![]() (
(![]() ), непрерывности магнитного потенциала
), непрерывности магнитного потенциала ![]() и индукции
и индукции ![]() на
границах при
на
границах при ![]() ,
, ![]() и
условия на бесконечности при
и
условия на бесконечности при ![]() :
:
![]() ,
,
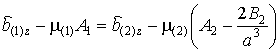 ,
,
![]() ,
(14)
,
(14)
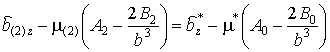 ,
,
![]() ;
;
из
последнего уравнения следует равенство ![]() .
.
Для рассматриваемой модели эффективная остаточная
макроиндукция ![]() магнитного поля композита будет
совпадать со средним значением индукции по составной двухфазной ячейке (11),
где
магнитного поля композита будет
совпадать со средним значением индукции по составной двухфазной ячейке (11),
где ![]() ,
, ![]() ‑
осредненные значения магнитной индукции по шару и по сферической оболочке
соответственно, константы
‑
осредненные значения магнитной индукции по шару и по сферической оболочке
соответственно, константы ![]() находим из решения
системы уравнений (14) с учетом (8).
находим из решения
системы уравнений (14) с учетом (8).
Опуская промежуточные выкладки, запишем полученное решение для эффективной остаточной магнитной индукции композита (12), где коэффициенты
объемная доля ![]() . Полученные решения (15) не зависят от
эффективной магнитной проницаемости
. Полученные решения (15) не зависят от
эффективной магнитной проницаемости ![]() композита, несмотря на
вхождение
композита, несмотря на
вхождение ![]() в систему уравнений (14). Отметим, что
решение для
в систему уравнений (14). Отметим, что
решение для ![]() получено ранее [5]
получено ранее [5]
Для частного случая, когда
![]() из (15), (16) следует решение
из (15), (16) следует решение
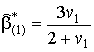 ,
,
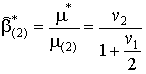 .
.
2.4 Составная сферическая ячейка
К такой расчетной схеме [5] приходим благодаря
однотипности и геометрического подобия всех составных сферических ячеек в
полидисперсной структуре на рис.1,а. Запишем соответствующие общие решения (6)
для каждой из двух областей рассматриваемой расчетной схемы – шар (1-я фаза,
включения композита) со сферической оболочкой (2-я фаза, матрица композита).
Константы интегрирования найдем из условий: ограниченности потенциала при ![]() (
(![]() ),
непрерывности магнитного потенциала
),
непрерывности магнитного потенциала ![]() и индукции
и индукции ![]() на границе при
на границе при ![]() и
условия
и
условия ![]() :
:
![]() ,
,
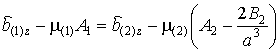 ,
(17)
,
(17)
![]()
Из решения системы уравнений (17) получим, что
аналитическое решение для эффективной остаточной магнитной индукции ![]() композита в точности совпадает с
полученным ранее решением (12), (15). Решение для эффективной магнитной
проницаемости
композита в точности совпадает с
полученным ранее решением (12), (15). Решение для эффективной магнитной
проницаемости ![]() композита также совпадает с
решением (16).
композита также совпадает с
решением (16).
Отметим,
что для случая ![]() имеем
имеем ![]() для
всех трех рассмотренных расчетных схем. В частности этот случай имеет место для
композита с взаимообратной начальной намагниченностью фаз, когда:
для
всех трех рассмотренных расчетных схем. В частности этот случай имеет место для
композита с взаимообратной начальной намагниченностью фаз, когда: ![]() ,
, ![]() , тогда
из (12), (15) следует решение
, тогда
из (12), (15) следует решение
![]()
3. Произвольная взаимная ориентация начальных магнитных индукций фаз композита
Решение для вектора ![]() в
случае произвольной взаимной ориентации векторов
в
случае произвольной взаимной ориентации векторов ![]() начальных
магнитных индукций фаз полидисперсных структур (рис.1) на основе принципа
суперпозиции представим суммой решений трех независимых осесимметричных по осям
начальных
магнитных индукций фаз полидисперсных структур (рис.1) на основе принципа
суперпозиции представим суммой решений трех независимых осесимметричных по осям
![]() ,
, ![]() ,
, ![]() задач с заданными начальными
намагниченностями фаз:
задач с заданными начальными
намагниченностями фаз: ![]() ,
, ![]() ,
, ![]() соответственно. Решение осесимметричной
по оси
соответственно. Решение осесимметричной
по оси ![]() задачи рассмотрено ранее (раздел 2),
решения двух других задач с осевой симметрией по осям
задачи рассмотрено ранее (раздел 2),
решения двух других задач с осевой симметрией по осям ![]() ,
,
![]() получим последовательной заменой индекса
получим последовательной заменой индекса ![]() в решении (раздел 2) соответственно на
в решении (раздел 2) соответственно на ![]() ,
, ![]() .
.
В результате искомые координаты
вектора
![]() остаточной магнитной индукции композита с
учетом (12), где координаты
остаточной магнитной индукции композита с
учетом (12), где координаты ![]() векторов
векторов ![]() начальных индукций фаз. Модуль
начальных индукций фаз. Модуль
![]()
и направляющие косинусы
![]()
вектора
![]() ,
,
где ![]() ‑
единичный направляющий вектор.
‑
единичный направляющий вектор.
4. Численный расчет
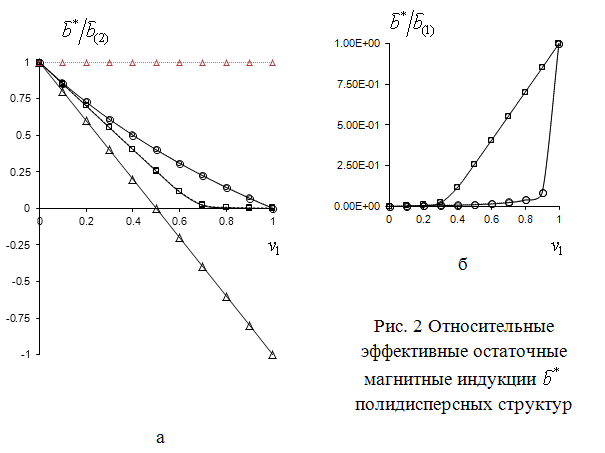
На
рис.2,а приведены результаты расчета влияния величины объемной доли ![]() сферических пор в магните на эффективные
остаточные магнитные индукции
сферических пор в магните на эффективные
остаточные магнитные индукции ![]() полидисперсных
структур на рис.1,а (
полидисперсных
структур на рис.1,а (![]() ) и на
рис.1,б (
) и на
рис.1,б (![]() ). Дополнительно
на рис.2,а результаты расчета для обеих структур (рис.1) с взаимообратной
намагниченностью фаз (
). Дополнительно
на рис.2,а результаты расчета для обеих структур (рис.1) с взаимообратной
намагниченностью фаз (![]() ). На рис.2,б ‑ эффективные остаточные
магнитные индукции
). На рис.2,б ‑ эффективные остаточные
магнитные индукции ![]() полидисперсных структур на
рис.1,а (
полидисперсных структур на
рис.1,а (![]() )
и на рис.1,б (
)
и на рис.1,б (![]() ) из сферических магнитов в воздухе.
) из сферических магнитов в воздухе.
Заключение
Получены новые решения (12), (13), (15) для
эффективных остаточных магнитных индукций различных: матричных (рис.1,а) и
кластерных (рис.1,б) полидисперсных структур со сферическими зернами
неоднородностями с учетом произвольной взаимной ориентации векторов начальных
магнитных индукций фаз (18). Доказано, что решение для остаточной магнитной
индукции ![]() матричной полидисперсной структуры на рис.1,а,
полученное на основе расчетной схемы: сферическое включение с прослойкой
матрицы в эффективной среде (12), (15) в точности совпадает с решением,
полученным на составной сферической ячейке (раздел 2.4). Отметим, что ранее [5]
аналогичные совпадения решений по разным расчетным схемам были отмечены,
например, для эффективного объемного модуля упругости и эффективной магнитной
проницаемости полидисперсной структуры на рис.1,а. Рассмотрены частные случаи:
намагниченные включения в эластомере, поры в намагниченной среде и
взаимообратная намагниченность фаз и представлены (рис.2) численные результаты
сравнительного анализа зависимостей эффективных остаточных магнитных индукций
различных намагниченных полидисперсных структур со сферическими включениями.
матричной полидисперсной структуры на рис.1,а,
полученное на основе расчетной схемы: сферическое включение с прослойкой
матрицы в эффективной среде (12), (15) в точности совпадает с решением,
полученным на составной сферической ячейке (раздел 2.4). Отметим, что ранее [5]
аналогичные совпадения решений по разным расчетным схемам были отмечены,
например, для эффективного объемного модуля упругости и эффективной магнитной
проницаемости полидисперсной структуры на рис.1,а. Рассмотрены частные случаи:
намагниченные включения в эластомере, поры в намагниченной среде и
взаимообратная намагниченность фаз и представлены (рис.2) численные результаты
сравнительного анализа зависимостей эффективных остаточных магнитных индукций
различных намагниченных полидисперсных структур со сферическими включениями.
Литература
1. Вонсовский С.В. Магнетизм. Магнитные свойства диа-, пара-, ферро-, антиферро- и ферримагнетиков. ‑ М.: Наука, 1971. ‑1032 с.
2. Чертович А.В., Степанов Г.В., Крамаренко Е.Ю. Магнитоуправляемые эластомеры: синтез, свойства, применение // XVII Зимняя школа по механике сплошных сред: сборник статей Международной научной конференции. ‑ Пермь, 2011. – С.328
3. Chertovich A.V., Stepanov G.V., Kramarenko E.Yu., Khokhlov A.R. New Composite Elastomers with Giant Magnetic Response // Macromolecular Materials and Engineering. – 2010. ‑ Vol. 295. ‑ pp. 336
4. Stolbov O. V., Raikher Yu. L., Balasoiu M. Modelling of magnetodipolar striction in soft magnetic elastomers // Soft Matter. – 2011. – No 7. ‑ pp. 8484-8487
5. Кристенсен Р. Введение в механику композитов. ‑ М.: Мир, 1982. ‑ 334 с.
6. Паньков А.А. Максвелл-вагнеровская релаксация в пьезокомпозите PVF/феррит с эллипсоидальными включениями в переменном электрическом поле // Журнал радиоэлектроники: электронный журнал. 2013. ‑ №6 . URL: http://jre.cplire.ru/jre/jun13/12/text.pdf
7. Паньков А.А. Влияние разупорядоченности и инверсии фаз на электромагнитную связанность пьезокомпозита с квазипериодической структурой // Журнал радиоэлектроники: электронный журнал. 2014. ‑ №1. URL: http://jre.cplire.ru/jre/jan14/12/text.pdf
8. Паньков А.А. Диэлектрическая релаксация в волокнистом композите полиэтилен/феррит // Журнал радиоэлектроники: электронный журнал. 2014. ‑ №2. URL: http://jre.cplire.ru/jre/feb14/1/text.pdf