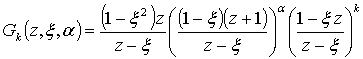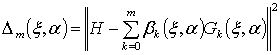УДК 681.518
ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ НЕОРТОГОНАЛЬНЫХ ФИЛЬТРОВ МЕЙКСНЕРА В СИСТЕМЕ GNU OCTAVE
И. М. Куликовских
Самарский национальный исследовательский университет
имени академика С.П. Королёва, Самара
Статья поступила в редакцию 17 апреля 2016 г., после доработки – 20 мая 2016 г.
Аннотация. В работе рассматриваются особенности вычисления коэффициентов неортогональных фильтров Мейкснера в системе GNU Octave. С этой целью приводится анализ вычисления коэффициентов с использованием встроенных функций Octave: quad, quadgk, quadcc, quadv, а также векторизованного аналога quadl. На основе проведенного анализа предлагается использование альтернативной векторизованной реализации вычисления коэффициентов, представленных в форме решения нормального уравнения. Предложенная реализация позволяет повысить эффективность и вычислительную устойчивость.
Ключевые слова: фильтры Мейкснера, векторизация вычислений, нормальное уравнение, квадратура.
Abstract. Previous research indicates that the Meixner filters can be a constructive alternative to the discrete Laguerre filters in signal processing applications. This may be explained by the impact of an extra parameter which allows providing better series expansion: it becomes possible to ensure the same approximation results using fewer terms. However, the orthogonal Meixner filters extensively studied so far either 1) have a rational z-transform only for even values of the extra parameter or 2) suggest synthesizing the Meixner filters from the Laguerre filters based on matrices transformation that leads to hardware redundancy. The primary focus of the present study is the nonorthogonal Meixner filters. In contrast to the previously discussed filters, these filters are rational for any integer value of the extra parameter and have a simple structure. But, it still seems that more attention needs to be drawn to the problem of expansions in nonorthogonal filters. This paper is aimed at considering the problem of computing the coefficients of the nonorthogonal Meixner filters with GNU Octave. To achieve this purpose, the study provides the analysis of computing the coefficients using build-in functions: quad, quadgk, quadcc, quadv as well as the vectorized representation of quadl. Based on the analysis results, the present research yields another vectorized representation of the coefficients in the form of normal equation to boost computational efficiency and to ensure numerical stability. In addition, the results of computations experiments confirmed the validity of the proposed vectorized representation to solve pole position problem for the nonorthogonal Meixner filters.
Key words: Meixner filters, vectorized computation, normal equation, quadrature.
Введение
Применение ортогональных фильтров для решения задач оценки характеристик динамических систем является общепринятым и широко используемым [1-5]. Как правило, ключевыми факторами при выборе вида фильтра являются простота реализации, разнообразие параметров адаптивной настройки и наличие алгоритмов оптимизации данных параметров.
В отличие от дискретных фильтров Лагерра [1-3,7], фильтры Мейкснера или обобщенные дискретные фильтры Лагерра имеют дополнительный параметр настройки фильтра. Как отмечает Нургес [8], данный параметр может быть использован для представления класса нестационарных линейных динамических систем. Авторы работ [9,10], в частности, выделяют полезность фильтров с дополнительным параметром для описания систем с запаздыванием, а именно, возможность получить ту же погрешность приближения при меньшем числе членов ряда.
Тем не менее, в явном виде z-преобразование функций Мейкснера [8-11] не является рациональным, что усложняет его физическую реализацию. В работе [9] предлагается z-преобразование функций, подобных функциям Мейкснера, которое позволяет реализовать рациональный фильтр, но лишь для четных значений дополнительного параметра. Фильтры Мейкснера, предложенные в работе [12], являются альтернативной формой представления обобщенных дискретных фильтров Лагерра или z-преобразования функций, подобных функциям Мейкснера [7,8]. Основным достоинством данных фильтров является рациональная форма представления для любых целочисленных значений дополнительного параметра и возможность представления динамических систем с дробным порядком [13] для нецелочисленных значений. Алгоритмы оптимизации параметров описываемых фильтров рассматривались в [14] и были обобщены и расширены до случая двухпараметрической оптимизации в [15]. Однако, особенность данных фильтров заключается в том, что для значения дополнительного параметра, отличного от нуля, они являются неортогональными и, следовательно, должны рассматриваться в контексте неортогональных систем базисных функций [16]. Для синтеза неортогональных фильтров требуется дополнительная операция, связанная с определением обратной матрицы, соответствующей скалярному произведению фильтров заданных порядков. Такая операция может привнести дополнительные вычислительные затраты при оценивании коэффициентов фильтров. Таким образом, целью данной работы является анализ различных способ реализации коэффициентов неортогональных фильтров Мейкснера. В качестве системы для программной реализации была выбрана свободная система для математических вычислений GNU Octave, имеющая интерпретируемый язык программирования, совместимый с MATLAB.
2. Неортогональные фильтры Мейкснера
Представим систему неортогональных фильтров Мейкснера ![]() для каждого заданного параметра
для каждого заданного параметра ![]() и действительного поля
и действительного поля ![]() в виде [12,14,15]:
в виде [12,14,15]:
Тогда, в предположении полноты системы ![]() на окружности радиусом в пределах
на окружности радиусом в пределах ![]() , зададим некоторую передаточную функцию
, зададим некоторую передаточную функцию ![]() , которая может быть представлена
ограниченным ортогональным рядом со следующей погрешностью приближения
, которая может быть представлена
ограниченным ортогональным рядом со следующей погрешностью приближения
где
коэффициенты неортогональных фильтров ![]() получены
из
получены
из ![]()
![]() (3)
(3)
с помощью следующего преобразования [16]:
![]() ,
,
откуда, с учетом (3),
![]() , (4)
, (4)
где
Перейдем к анализу вычисления (1), (4) и (5) в системе GNU Octave.
3. Анализ способов вычисления коэффициентов в GNU Octave
GNU Octave [17] создавался с учетом совместимости с MATLAB и по большей части реализует его возможности. Однако, часть функций, представленных в MATLAB, являются пока отсутствующим функционалом в Octave либо их вычисление представляет собой некоторую специфику. В частности, для вычисления квадратур в Octave представлены следующие функции quad, quadgk, quadcc, quadv, quadl, trapz, cumtrapz [18]. В данной работе мы опустим рассмотрение квадратур, реализующих метод трапеций trapz, cumtrapz, так как, согласно прилагаемой документации [18], данные квадратуры, в первую очередь, предназначены для работы с эмпирическими данными, чем с функциями.
Следует также отметить специфику, связанную с вычислением квадратуры quadl, реализующей метод Гаусса-Лобатто [19,20]. Octave-версия данной функции при большом значении допустимой погрешности tol не сходится [20]. Для компенсации данного недостатка необходимо внести соответствующие изменения в код quadl.m согласно [21]. В рамках данной работы для проведения сравнительного анализа предлагается рассмотреть реализацию метода Гаусса-Лобатто, представленную в [19]. Данная версия алгоритма является векторизованным аналогом, следовательно, требует меньших временных затрат на получение конечного результата. При проведении сравнительного анализа для данной квадратуры используется название vectGL.
4. Экспериментальные исследования
При проведении экспериментальных исследований использовался MacBook Air 11 OS X EI Captain с процессором 1.3 GHz Intel Core i5 и памятью 4 GB 1600 MHz DDR3, а также GNU Octave 3.8.2.
Как видно из формулы (1), параметр ![]() не
оказывает существенного влияния на вычислительные затраты. Особые случаи могут
быть связаны лишь с вычислением определенного вида квадратур на границах
интервала определенности
не
оказывает существенного влияния на вычислительные затраты. Особые случаи могут
быть связаны лишь с вычислением определенного вида квадратур на границах
интервала определенности ![]() . Следовательно, в
целях общности подхода влияние параметра
. Следовательно, в
целях общности подхода влияние параметра ![]() в
рамках текущего эксперимента рассматриваться не будет. Параметр
в
рамках текущего эксперимента рассматриваться не будет. Параметр ![]() , в свою очередь, оказывает влияние,
аналогичное изменению параметра
, в свою очередь, оказывает влияние,
аналогичное изменению параметра ![]() , но может также иметь
специфику для ряда квадратур при выборе нецелочисленных значений. Таким
образом, сфокусируемся на анализе влияния числа членов
, но может также иметь
специфику для ряда квадратур при выборе нецелочисленных значений. Таким
образом, сфокусируемся на анализе влияния числа членов ![]() .
.
В качестве аппроксимируемой функции
выбрана передаточная функция впуска сверхзвукового реактивного двигателя,
рассмотренная в [7,14,15]. Зададим ![]() ,
, ![]() ,
, ![]() . Для
вычисления векторизованной квадратуры Гаусса-Лобатто примем
. Для
вычисления векторизованной квадратуры Гаусса-Лобатто примем ![]() , выбранная допустимая погрешность
встроенных квадратур
, выбранная допустимая погрешность
встроенных квадратур ![]() . Для оценки качества работы
алгоритмов предлагается анализировать погрешность вычисления матрицы скалярного
произведения фильтров (5). Данная матрица с учетом нормирования должна быть
единичной, так как при
. Для оценки качества работы
алгоритмов предлагается анализировать погрешность вычисления матрицы скалярного
произведения фильтров (5). Данная матрица с учетом нормирования должна быть
единичной, так как при ![]() система фильтров является
ортогональной. Для оценки временных затрат на вычисление каждой квадратуры воспользуемся
функциями tic,
toc. В
таблице 1 представлены численные значения результатов проведенных
экспериментов.
система фильтров является
ортогональной. Для оценки временных затрат на вычисление каждой квадратуры воспользуемся
функциями tic,
toc. В
таблице 1 представлены численные значения результатов проведенных
экспериментов.
Таблица 1. Результаты экспериментальных исследований
|
m |
Вид квадратуры |
Погрешность |
Время, с |
|
5 |
quad |
-4.8252e-16 |
0.693273 |
|
quadgk |
2.2470e-16 |
0.118194 |
|
|
quadcc |
-1.7437e-15 |
6.04893 |
|
|
quadv |
1.0779e-15 |
0.660079 |
|
|
vectGL |
7.7913e-16 |
0.056676 |
|
|
10 |
quad |
-5.8988e-15 |
1.98472 |
|
quadgk |
2.0969e-16 |
0.270076 |
|
|
quadcc |
-3.5335e-15 |
206.763 |
|
|
quadv |
6 |
1.50241 |
|
|
vectGL |
1.7871e-15 |
0.08419 |
|
|
20 |
quad |
-2.1291e-14 |
7.61214 |
|
quadgk |
9.2062e-16 |
0.96911 |
|
|
quadcc |
- |
- |
|
|
quadv |
- |
- |
|
|
vectGL |
3.5146e-16 |
0.138862 |
|
|
35 |
quad |
-8.0526e-14 |
26.0142 |
|
quadgk |
1.1215e-14 |
3.09233 |
|
|
quadcc |
- |
- |
|
|
quadv |
- |
- |
|
|
vectGL |
-4.1262e-16 |
0.28536 |
Как видно из таблицы, среди встроенных функций наилучшие результаты получены для quadgk, что было ожидаемым, так как данная квадратура признана одной из наиболее эффективных в среде MATLAB. В свою очередь, quadv выдала некорректный результат уже при 10 членах ряда и при увеличении m погрешность продолжала расти, что отмечено прочерками в таблице. Другое выявленное несоответствие – существенное увеличение времени вычислений для quadcc. Данная квадратура не представляет дальнейшего интереса в рамках поставленной задачи, что также было отмечено прочерками.
Векторизованная квадратура Гаусса-Лобатто vectGL продемонстрировала наилучшие результаты. Однако, практика показывает, что в сравнительном анализе quadgk и встроенной квадратуры MATLAB quadl, quadgk дает более устойчивые и стабильные решения. Следовательно, необходимо предложить более эффективное решение, которое бы показывало стабильные результаты при малых вычислительных затратах.
5. Вычисление коэффициентов в виде решения нормального уравнения
В качестве альтернативного решения предлагается вычислять коэффициенты, исходя из нормального уравнения.
Представим погрешность (2) в матричном виде
![]() ,
, ![]() ,
,
![]() ,
,
где
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Тогда,
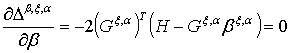 ,
,
откуда получаем нормальное уравнение
![]() .
.
Следовательно, коэффициенты могут быть представлены в следующей форме
![]() . (6)
. (6)
Представим сравнительный анализ предложенного выше подхода к
вычислению коэффициентов normEq (6),
векторизованного метода Гаусса-Лобатто vectGL и встроенной функции quadgk в виде графической зависимости
временных затрат от числа членов m (см.
рис. 1). Метод normEq был
реализован для ![]() , что определяет число значащих
цифр при оценке коэффициентов. Диапазон изменения числа членов
, что определяет число значащих
цифр при оценке коэффициентов. Диапазон изменения числа членов ![]() (от 10 до 70 с шагом 10). Следует
отметить, что, как правило, выбор настолько большого значения m не требуется. Тем не менее, задача
синтеза фильтров не ограничивается лишь расчетом коэффициентов: при оптимизации
параметров фильтра вычисление коэффициентов часто выполняется в циклах. Таким
образом, цель данного эксперимента – оценить временные затраты при многократном
вызове функций quadgk, vectGL и normEq.
(от 10 до 70 с шагом 10). Следует
отметить, что, как правило, выбор настолько большого значения m не требуется. Тем не менее, задача
синтеза фильтров не ограничивается лишь расчетом коэффициентов: при оптимизации
параметров фильтра вычисление коэффициентов часто выполняется в циклах. Таким
образом, цель данного эксперимента – оценить временные затраты при многократном
вызове функций quadgk, vectGL и normEq.
Как видно из рисунка, normEq требует меньших временных затрат при ![]() . При увеличении данного значения время
возрастает, но незначительно. Однако, явным достоинством normEq по сравнению с vectGL является большая устойчивость к
изменениям параметров фильтра.
. При увеличении данного значения время
возрастает, но незначительно. Однако, явным достоинством normEq по сравнению с vectGL является большая устойчивость к
изменениям параметров фильтра.
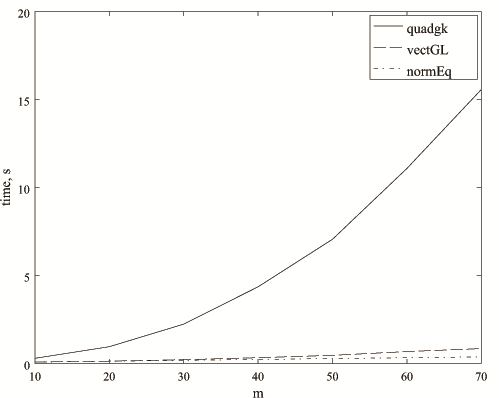
Рис. 1. Графические зависимости времени вычисления коэффициентов
от числа членов ряда для функций quadgk, vectGL, normEq
Проведем сравнительный анализ vectGL и normEq при вычислении коэффициентов фильтра
на всей области определения ![]() и фиксированных
значениях
и фиксированных
значениях ![]() ,
, ![]() .
Результаты данного вычислительного эксперимента представлены на рис. 2.
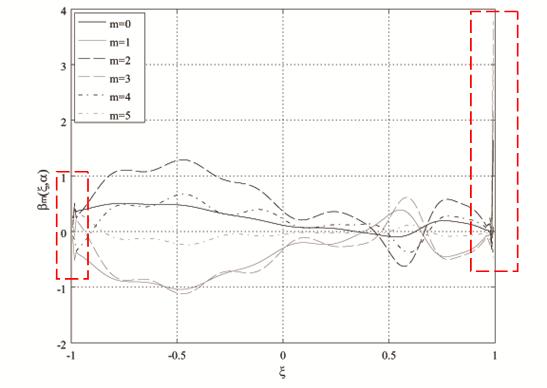
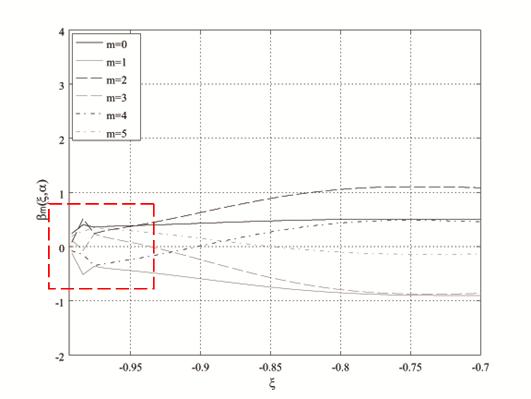
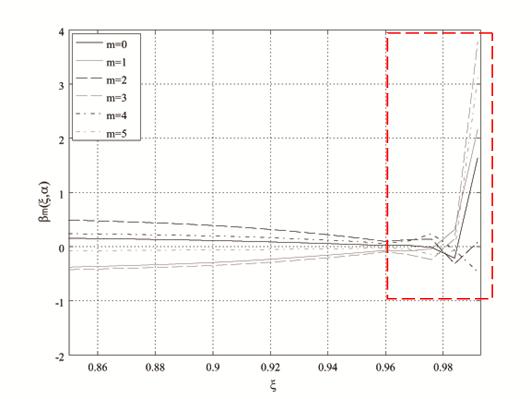
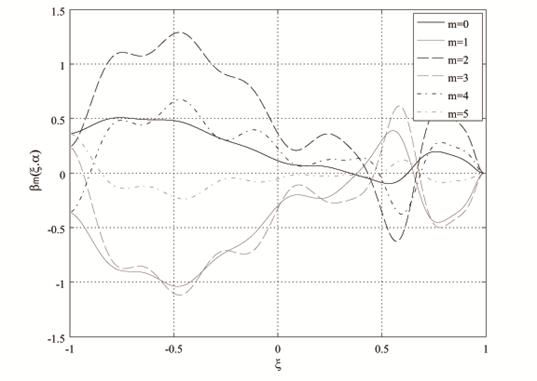
Полученные результаты показывают, что при использовании vectGL (рис. 2 (а)) были выявлены погрешности
на границах интервала
.
Результаты данного вычислительного эксперимента представлены на рис. 2.
Полученные результаты показывают, что при использовании vectGL (рис. 2 (а)) были выявлены погрешности
на границах интервала ![]() (рис. 2 (б, в)), в то время как
normEq выдал устойчивое решение (рис. 2 (г)).
Если оптимальное значение параметра
(рис. 2 (б, в)), в то время как
normEq выдал устойчивое решение (рис. 2 (г)).
Если оптимальное значение параметра ![]() располагается близко к
границе интервала, то данная разница между двумя методами может оказаться
критической.
располагается близко к
границе интервала, то данная разница между двумя методами может оказаться
критической.
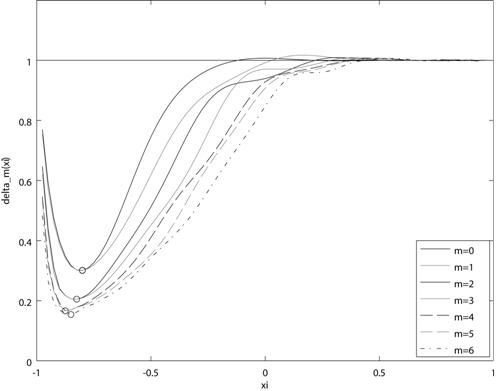
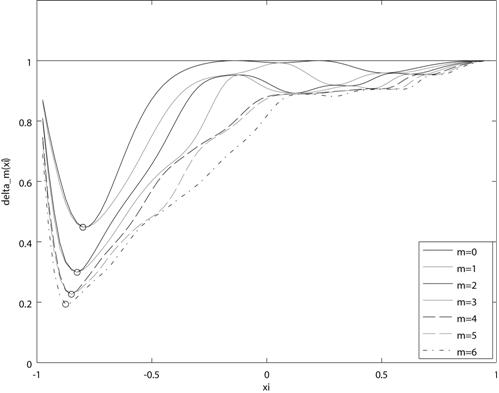
Влияние выявленных погрешностей при
оценке коэффициентов может быть продемонстрировано на примере решения задачи
оптимизации параметра ![]() при тех же фиксированных
значениях
при тех же фиксированных
значениях ![]() ,
, ![]() . На
рис. 3 приведены кривые нормированных погрешностей, определяемых исходя из
выражения
. На
рис. 3 приведены кривые нормированных погрешностей, определяемых исходя из
выражения ![]() : (а) соответствует вычислению
коэффициентов с помощью vectGL; (б) – использованию normEq.
: (а) соответствует вычислению
коэффициентов с помощью vectGL; (б) – использованию normEq.
|
(а) |
(б) |
|
(в) |
(г) |
Рис. 2. Графические зависимости ![]() при
при ![]() и
и ![]()
при использовании: (а) vectGL; (б) vectGL (левая граница ![]() );
);
(в) vectGL (правая граница ![]() ); (г)
normEq
); (г)
normEq
|
(а) |
(б) |
Рис. 3. Графические зависимости
относительной погрешности ![]() : (а) vectGL; (б) normEq
: (а) vectGL; (б) normEq
Как видно из рис. 3 (а), полученные кривые нормированных
погрешностей в диапазоне ![]() превышают единицу в
отличие от приведенных на рис. 3 (б). Следует также заметить, что форма кривых
и отмеченные маркерами оптимальные значения параметра
превышают единицу в
отличие от приведенных на рис. 3 (б). Следует также заметить, что форма кривых
и отмеченные маркерами оптимальные значения параметра ![]() существенным
образом отличаются от полученных с помощью normEq (рис. 3 (б)). В свою очередь, форма
кривых и значения, отмеченные маркером на рис. 3 (б), точно совпадают с
аналитическим решением задачи оптимизации, предложенным в работах [14,15].
существенным
образом отличаются от полученных с помощью normEq (рис. 3 (б)). В свою очередь, форма
кривых и значения, отмеченные маркером на рис. 3 (б), точно совпадают с
аналитическим решением задачи оптимизации, предложенным в работах [14,15].
6. Выводы
В работе рассмотрены различные способы вычисления коэффициентов неортогональных фильтров Мейкснера в системе GNU Octave. В результате проведенного сравнительного анализа встроенных функций для вычисления квадратур quad, quadgk, quadcc, quadv и векторизованного метода Гаусса-Лобатто vectGL был сделан следующий вывод: среди встроенных функций наилучшие результаты были получены с использованием quadgk; среди всех анализируемых квадратур лучший результат показал векторизованный метод vectGL. Учитывая тот факт, что квадратура Гаусса-Лобатто в общем случае чувствительна к изменениям параметров и, таким образом, является менее устойчивой, была предложена альтернативная векторизованная реализация вычисления коэффициентов, представленных в форме решения нормального уравнения normEq. Эффективность предложенной реализации была подтверждена экспериментально.
Финансирование
Работа выполнена при государственной поддержке Министерства образования и науки РФ (грант № 074-U01).
Литература
1. Ю. Нургес Синтез регулятора на лагерровой модели. // Автомат. и телемех., 1994, №4, С. 47-54.
2. С. А. Прохоров Аппроксимативный анализ случайных процессов. – Самара: СНЦ РАН, 2001, – 380 с.
3. А. А. Бессонов, Ю. В. Загашвили, А. С. Маркелов Методы и средства идентификации динамических объектов. – Л.: Энергоатомиздат, 1989, – 280 с.
4. Л. В. Кузьмин, Р. Ю. Емельянов Система ортогональных сигналов для некогерентного приема сверхширокополосных хаотических радиоимпульсов в многолучевом канале. // Журнал радиоэлектроники: электронный журнал. 2014. №7. URL: http://jre.cplire.ru/iso/jul14/1/text.pdf
5. Д. А. Балакин, В. В. Штыков Построение ортогонального банка фильтров на основе преобразований Эрмита для обработки сигналов. // Журнал радиоэлектроники: электронный журнал. 2014. №8. URL: http://jre.cplire.ru/iso/sep14/1/text.pdf
6. А. Е. Нивин, А. В. Саушев, В. А. Шошмин Синтез ортогональных фильтров при статистической идентификации динамических систем. // Известия вузов. Приборостроение, 2013, № 10(56), С. 5-10.
7. M. Telescu, N. Iassamen, P. Cloastre, N. Tanguy A simple algorithm for stable order reduction of z-domain Laguerre models. // Signal Processing, 2013, vol. 93, pp. 332-337.
8. Ю. Нургес Модели Мейкснера линейных дискретных систем. // Автомат. и телемех., 1988, №12, С. 128-136.
9. A. C. den Brinker Meixner-like functions having a rational z-transform. // Int. J. Circuit Theory Appl., 1995, vol. 23, pp. 237-246.
10. H. J. W. Belt Orthogonal basis for adaptive filtering (Ph.D. thesis), Eindhoven University of Technology, May 1997.
11. J. Meixner Orthogonale polynomsysteme mit einer besonderen gestalt der erzeugenden funktion. // J. Lond. Math. Soc., 1934, 9, pp. 6-13.
12. S. A. Prokhorov, I. M. Kulikovskikh Unique condition for generalized Laguerre functions to solve pole position problem. // Signal Processing, 2015, vol. 108, pp. 25-29.
13. А. Г. Бутковский, С. С. Постнов, Е. А. Постнова Дробное интегрально-дифференциальное исчисление и его приложения в теории управления. II. Дробные динамические системы: моделирование и аппаратная реализация. // Автомат. и телемех., 2013, №5, С. 3-34.
14. С. А. Прохоров, И. М. Куликовских Условие оптимальности фильтров Мейкснера. // Журнал радиоэлектроники: электронный журнал. 2015. №4. URL: http://jre.cplire.ru/mac/apr15/9/text.html
15. S. A. Prokhorov, I. M. Kulikovskikh Pole position for Meixner filters. // Signal Processing, 2016, vol. 120, pp. 8-12.
16. W. H. Klink, G. L. Payne Approximating with nonorthogonal basis functions. // J. Comput. Phys., 1976, vol. 21, pp. 208-226.
17. GNU Octave https://www.gnu.org/software/octave/ (дата обращения 14.04.2016).
18. Численное интегрирование. Функции одной переменной http://www.gnu.org/software/octave/doc/v4.0.1/Functions-of-One-Variable.html (дата обращения 14.04.2016).
19. P. Getreuer Writing fast MATLAB code, February 2009.
20. W. Gander, W. Gautschi Adaptive quadrature –Revisited. // BIT, 2000, №1 (40), pp. 84-101.
21. Octave changeset http://hg.savannah.gnu.org/hgweb/octave/rev/85dac13a911b (дата обращения 14.04.2016).
References
1. Nurges U. A. Synthesis of regulator using Laguerre model. Automation Remote Control. 1994, Vol. 49, p. 1638-1644.
2. Prokhorov S. A. Approksimativnyj analiz sluchajnyh processov. [Approximative analysis of stochastic processes]. Samara, SNC RAN Publ. 2001. 380 p. (In Russian)
3. Bessonov A. A., Zagashvili Y. V., Markelov A.S. Metody i sredstva identifikacii dinamicheskih objektov. [Methods and tools for dynamic system identification]. Leningrad, Energoizdat Publ. 1989. 280 p. (In Russian)
4. Kyzmin L. V., Emelyanov R. Y. System of orthogonal signals for noncoherent receiving of ultrawideband chaotic radiopulses in multipath channel. Zhurnal Radioelektroniki - Journal of Radio Electronics, 2014, No. 7. Available at http://jre.cplire.ru/iso/jul14/1/text.pdf. (In Russian)
5. Balakin D. A., Shtykov V. V. The construction of orthogonal filters bank based on Hermit transform for signal processing. Zhurnal Radioelektroniki - Journal of Radio Electronics, 2014, No. 9. Available at http://jre.cplire.ru/iso/sep14/1/text.pdf. (In Russian)
6. Nivin А. Е., Saushev А. V., Shoshmin V. А. Synthesis of orthogonal filters in statistical identifications of dynamic system. Izvestiya vysshikh uchebnykh zavedeniy Priborostroenie - Journal of Instrument Engineering, 2013, Vol. 56, No. 10, pp. 5-10. (In Russian)
7. Telescu M., Iassamen N., Cloastre P., Tanguy N. A simple algorithm for stable order reduction of z-domain Laguerre models. Signal Processing, 2013, Vol. 93, pp. 332-337.
8. Nurges U. A. Meixner models of linear discrete systems. Automation Remote Control, 1988, No. 49, p. 128-136.
9. Den Brinker A. C. Meixner-like functions having a rational z-transform. Int. J. Circuit Theory Appl., 1995, Vol. 23, pp. 237-246.
10. Belt H. J. W. Orthogonal basis for adaptive filtering (Ph.D. thesis), Eindhoven University of Technology, May 1997.
11. Meixner J. Orthogonale polynomsysteme mit einer besonderen gestalt der erzeugenden funktion. J. Lond. Math. Soc., 1934, Vol. 9, pp. 6-13.
12. Prokhorov S. A. , Kulikovskikh I. M. Unique condition for generalized Laguerre functions to solve pole position problem. Signal Processing, 2015, Vol. 108, pp. 25-29.
13. Butkovskii A. G., Postnov S. S., Postnova E. A. Fractional integro-differential calculus and its control-theoretical applications. II. Fractional dynamic systems: Modeling and hardware implementation. Automation Remote Control, 2013, Vol. 74, No. 5, pp. 725-749.
14. Prokhorov S. A., Kulikovskikh I. M. Optimality condition for Meixner filters. Zhurnal Radioelektroniki - Journal of Radio Electronics, 2015, No. 4. Available at http://jre.cplire.ru/mac/apr15/9/text.pdf. (In Russian)
15. Prokhorov S. A., Kulikovskikh I. M. Pole position problem for Meixner filters. Signal Processing, 2016, Vol. 120, pp. 8-12.
16.
Klink W. H., Payne G. L. Approximating with nonorthogonal basis functions.
J. Comput. Phys., 1976, Vol. 21, pp. 208-226.
17. GNU Octave. Available at https://www.gnu.org/software/octave/. Accessed 14.04.2016.
18. Numerical Integration. Functions of one variable. Available at http://www.gnu.org/software/octave/doc/v4.0.1/Functions-of-One-Variable.html. Accessed 14.04.2016.
19. Getreuer P. Writing fast MATLAB code, February 2009. Available at http://www.ee.columbia.edu/~marios/matlab/Writing_Fast_MATLAB_Code.pdf. Accessed 14.04.2016.