|
|
"ÆÓÐÍÀË ÐÀÄÈÎÝËÅÊÒÐÎÍÈÊÈ" N 4, 2002 |
|
On a Possibility to Decrease Magnetic Intensity in Microwave/DC Cyclotron Wave Converter
Vladimir A. Vanke, e-mail: vanke@mesps.phys.msu.su
Moscow State University
Hiroshi Matsumoto and Naoki Shinohara
Kyoto University, Japan
Received on April 15, 2002
I. Introduction
In connection with successfully developing ideas of Wireless Power Transportation (WPT) there appeared a new problem, namely, the problem of back conversion of high-power microwave energy in the energy of direct current.
The most studied cyclotron wave converter (CWC) is potentially powerful, already tested at different power levels up to 10 kW and rather well known from the previous publications [1-3, etc].
However such type of CWC demands magnetic intensity, which corresponds to the cyclotron frequency wc equal to the frequency w of external microwave power source. This requirement (wc = w) usually creates essential technical problems, especially in the short centimetric and millimetric wavebands.
This article discusses another type of CWC [4,5], which uses two microwave cavities having uniform and quadruple electric fields in the interaction gaps which makes it possible to reduce the magnetic intensity in two times.
II. Principle of Operation
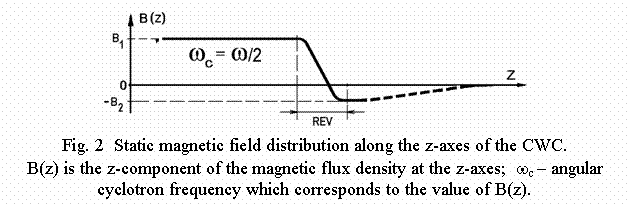
Fig. 1 and Fig. 2 illustrate a schematic view of such CWC tube and static magnetic field distribution along the z-axis, respectively.
Electron gun 1 forms an electron beam 2 of a round cross-section, which is injected along the z-axis into the first cavity having potential equal to the potential of source 12, i.e. U, because at the normal operational mode the current in resistor 13 is absent.
The first microwave cavity 3 has resonant frequency equal to a half of the frequency w of incoming microwave power P. A small part of this power (<1%) via power splitter 6, frequency divider 5 and phase shifter 4 feeds cavity 3. Transverse electric field in the gap of interaction of the cavity 3 in combination with the resonant static and uniform magnetic field (wc = w /2, see Fig. 2) creates a small initial rotation of the electron beam around the z-axes.
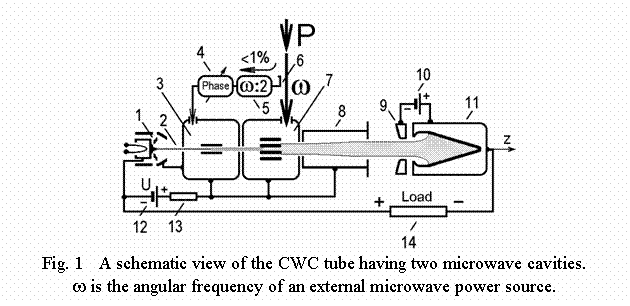
The second microwave cavity 7 has resonant frequency equal to the frequency w and quadruple type of the electric field in the gap of interaction. At the same magnetic field (wc = w /2) such quadruple field can accelerate or decelerate transverse rotation of the beam depending on initial (inlet) phase. Phase shifter 4 makes it possible to fix an optimal phase at which initial radius of beam rotation will increase and energy of external microwave source will effectively convert into the energy of electron beam rotation around the z-axis.
A drift tube 8 has the same potential U (see Fig. 1) but static magnetic field is changed here in both the direction and the magnitude (region “REV” in Fig. 2). The longitudinal velocity of rotating electron beam is increased in the divergent magnetic field of this region. Radial component of static magnetic field creates the process when energy of electron beam rotation is transferred into the additional energy of its longitudinal motion. Simultaneously, the electron beam configuration is changed - it takes shape of a spatial helix (energy of fast cyclotron wave [6] is transferred into the energy of synchronous wave [6] of the same polarization). It is important to emphasize that optimal energy conversion in this region takes place always in asymmetrically reversed magnetic field (value of B2 less then value of B1 in Fig. 2) for any real technical parameters of CWC [1].
After reverse region the accelerated electron beam enters collector region where its kinetic energy is recuperated and transformed in d.c. energy which appears at the load resistance 14. Magnetic field distribution here depends on concrete collector construction and usually has a shape of decreasing field as it is shown approximately in Fig. 2 by dashed line. Additional electrode 9 is fed by voltage source 10 and has potential a bit lower than the potential of the collector 11. This additional electrode 9 creates a local electric field just at the collector orifice, which protects against outcoming of the secondary emitted electrons.
Resistor 13 creates a simple current limiting system. Any small current (caused by microwave or d.c. overloads) to the walls of the elements 3, 7, 8 will drop essentially in potential of them and decrease electron gun current.
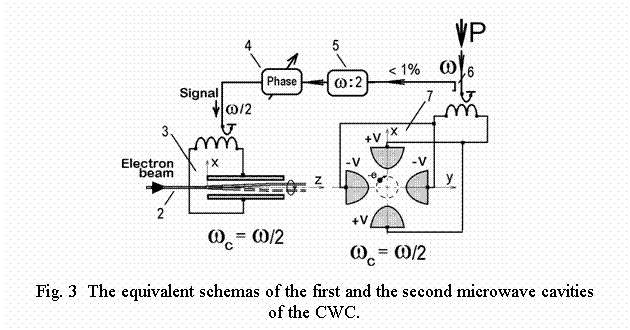
Fig. 3 shows the equivalent schemas of the microwave cavities 3 and 7. The interaction gap of the first of them is shown along the z-axes (y = 0 plane), the quadruple gap of the second cavity is given as a picture across the z-axes (z = const plane). The cavities have different resonant frequencies, different electrode configuration, different equivalent capacities and inductivities. The first cavity 3 creates a small initial rotation of the electron beam at the frequency equal to w /2. Such initial rotation is necessary for the interaction in the second cavity having electric field intensity equal to zero at the axes of the quadruple field. Fig. 3 shows the electrode potentials +V, -V at some fixed moment of time. Electron beam cross-section is shown as a bold black point “-e” and corresponds to the optimal phase (y = - x for the center of this beam cross-section), which can be installed by phase shifter 4. The motion trajectory of the beam cross-section is a circle, shown by dashed line.
III. Efficiency of Quadruple Cavity
Using the equivalent parallel conductivity terminology one can write for the efficiency of microwave energy conversion by quadruple cavity into the energy of the fast cyclotron wave [6] of the electron beam
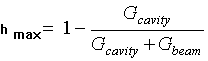 , (1)
, (1)
where
![]() - the active equivalent parallel
conductivity of the quadruple cavity caused by Joule’s losses,
- the active equivalent parallel
conductivity of the quadruple cavity caused by Joule’s losses,
![]() - the
active part of the equivalent parallel conductivity caused by the interaction
of the electron beam
- the
active part of the equivalent parallel conductivity caused by the interaction
of the electron beam
and quadruple electric field of the cavity.
Let us take the quadruple potential distribution inside the gap of interaction (Fig. 3) in a typical form
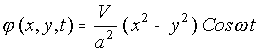 ,
(2)
,
(2)
where ![]() - the minimal distance between the z-axes
and a quadruple electrode.
- the minimal distance between the z-axes
and a quadruple electrode.
If the resonant condition is fulfilled (vc = v/2), the inlet phase is equal to the optimal one (y = - x for the center of the beam cross-section in Fig. 3) and the interaction has an adiabatic type, it is not very difficult to obtain that
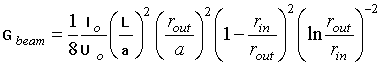 , (3)
, (3)
where
- the electron beam current,
- the electron beam potential,
- the length of the quadruple field region,
- the radius of rotation of the center of the electron beam cross-section at the
inlet f the quadruple region,
- the same one at the outlet of the quadruple region.