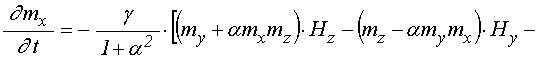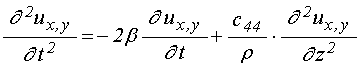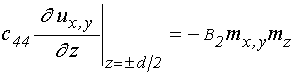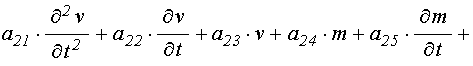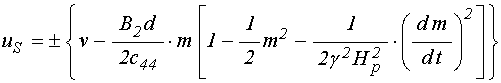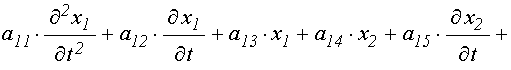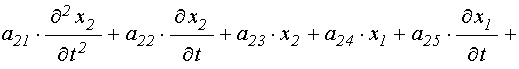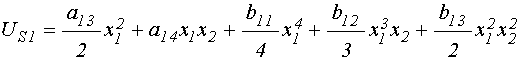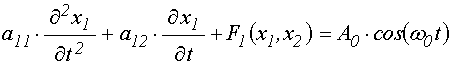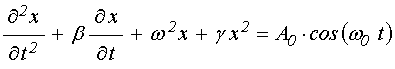УДК 537.874; 537.624
АНАЛИЗ АВТОМОДУЛЯЦИОННЫХ ЯВЛЕНИЙ В СИСТЕМЕ СВЯЗАННЫХ МАГНИТНОГО И УПРУГОГО ОСЦИЛЛЯТОРОВ НА ОСНОВЕ МОДЕЛИ ПОТЕНЦИАЛА
А. П. Иванов1, В. Г. Шавров2, В. И. Щеглов2
1 Сыктывкарский государственный университет
2 Институт радиотехники и электроники им. В.А. Котельникова РАН
Статья получена 7 июня 2015 г.
Аннотация. Рассмотрены нелинейные вынужденные колебания намагниченности и упругого смещения в нормально намагниченной ферритовой пластине, обладающей магнитоупругими свойствами. Задача сведена к модельной системе из двух связанных осцилляторов, имеющей две с половиной степени свободы. Рассмотрены два вида связи между осцилляторами – через переменные и через производные. Для связи через переменные получен потенциал кубического вида с потенциальным барьером. Рассмотрено возбуждение колебаний автомодуляционного характера. Построена модель фазовой задержки, объясняющая явление автомодуляции малой скоростью движения осциллятора вблизи вершины потенциального барьера. Рассмотрены условия возбуждения двухамплитудных и квазихаотических колебаний, а также ухода системы на бесконечность.
Ключевые слова: магнитоупругое взаимодействие, нелинейные колебания, автомодуляционный режим.
Abstract. The nonlinear forced vibrations of magnetization and elastic displacement in normal magnetized ferrite plate having magnetoelastic properties are investigated. The task is transformed to model system of two connected oscillators having two and a half freedom degree. Two classes of between-oscillator connection – through variable quantities and through derivatives are investigated . For the connection through variable quantities it is found the cubic potential with potential barrier. The excitation of auto-modulated vibrations is investigated. It is created the model of phase delay which explains the auto-modulation phenomenon by small velocity of oscillator near the top of potential barrier. The conditions of excitation of two-amplitude and quasi-chaotic vibrations and also the motion of system to infinity are investigated.
Key words: magnetoelastic interaction, nonlinear vibrations, auto-modulation regime.
Введение
Возбуждение ультразвуковых колебаний с
помощью магнитострикционных преобразователей издавна привлекает внимание исследователей
[1-8]. Особый интерес представляет использование таких преобразователей в диапазоне
СВЧ (![]() ), где высокая механическая добротность ферритовых
резонаторов (до
), где высокая механическая добротность ферритовых
резонаторов (до ![]() ) позволяет создать весьма эффективные
устройства обработки информации [9,10]. Важнейшей задачей здесь является создание
достаточно эффективного излучателя гиперзвука, определенным препятствием к чему
может явиться нелинейное параметрическое возбуждение обменных спиновых волн
[11-13]. Однако в работах [14-18] показано, что параметрический распад можно предотвратить
путем выбора геометрии преобразователя в виде нормально намагниченной тонкой пластины.
) позволяет создать весьма эффективные
устройства обработки информации [9,10]. Важнейшей задачей здесь является создание
достаточно эффективного излучателя гиперзвука, определенным препятствием к чему
может явиться нелинейное параметрическое возбуждение обменных спиновых волн
[11-13]. Однако в работах [14-18] показано, что параметрический распад можно предотвратить
путем выбора геометрии преобразователя в виде нормально намагниченной тонкой пластины.
Наряду с работами, касающимися линейного возбуждения гиперзвука в такой структуре [9,10,19], в работе [20] было показано, что нелинейный режим позволяет повысить уровень возбуждения гиперзвука на два порядка. Потребность упрощения сложного математического аппарата работы [20] привела к созданию модели, рассматривающей возбуждение гиперзвука на основе нелинейных колебаний связанных магнитного и упругого осцилляторов в линейном и квадратичном приближении [21-24].
В работах [25-29] было показано, что в такой системе, наряду со стационарным возбуждением колебаний постоянной амплитуды, возможны автомодуляционные режимы, в которых амплитуда колебаний меняется как периодически, так и хаотическим образом. В работе [30] показана возможность возбуждения таких колебаний в случае, когда один из осцилляторов является нелинейным, а другой – линейным, причем связь между осцилляторами имеет нелинейный характер. На основе анализа разверток во времени и параметрических портретов выявлены пять основных режимов автомодуляционных колебаний, сменяющие друг друга по мере увеличения амплитуды возбуждения: регулярный синусоидальный, регулярный с расщеплением, регулярный без расщепления, нерегулярный квазихаотический и нерегулярный расходящийся.
Для интерпретации наблюдаемых явлений предложена модель обобщенного потенциала, имеющего вид суммы степенных функций, образованных произведениями координат обоих осцилляторов. На основе геометрии потенциальной поверхности проанализирована роль отдельных слагаемых в формировании регулярных режимов колебаний, а также выявлены условия, обеспечивающие уход системы на бесконечность. Для интерпретации наблюдаемого в одном из режимов расщепления синусоидальных колебаний предложена модель генерации гармоник за счет нелинейности системы.
Однако такая модель, давая качественную интерпретацию, носит эмпирический описательный характер, не позволяя раскрыть как механизм, так и последовательность формирования расщепления.
В общем характере вынужденных колебаний не выявлена взаимная роль первого и второго осцилляторов, отсутствует сопоставление вынужденных колебаний со свободными, не рассмотрена последовательность развития во времени как расщепления, так и установления стационарных режимов.
Настоящая работа является продолжением [30] и также посвящена применению модели потенциала к интерпретации автомодуляционных явлений. Значительное внимание уделяется разработке обобщенного математического аппарата на основе положений общей теории нелинейных колебаний.
1. Геометрия задачи и основные уравнения
Геометрия задачи, совпадающая
с принятой в [30] и предшествующих работах, показана на рис.1. В ее основе лежит
плоскопараллельная пластина толщины ![]() , обладающая магнитными,
упругими и магнитоупругими свойствами. Материал пластины имеет кубическую кристаллографическую
симметрию, плоскость (100) которой совпадает с плоскостью пластины.
, обладающая магнитными,
упругими и магнитоупругими свойствами. Материал пластины имеет кубическую кристаллографическую
симметрию, плоскость (100) которой совпадает с плоскостью пластины.
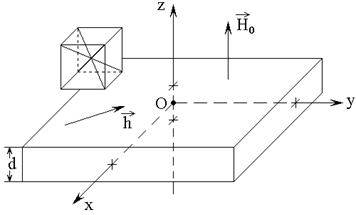
Рис.1. Геометрия задачи. Слева – схема кристаллографической ячейки.
Внешнее постоянное магнитное
поле ![]() приложено перпендикулярно плоскости пластины,
переменное магнитное поле
приложено перпендикулярно плоскости пластины,
переменное магнитное поле ![]() действует в плоскости пластины.
Задача решается в декартовой системе координат
действует в плоскости пластины.
Задача решается в декартовой системе координат ![]() , плоскость
, плоскость
![]() которой совпадает с плоскостью пластины, а
оси
которой совпадает с плоскостью пластины, а
оси ![]() ,
, ![]() и
и ![]() параллельны ребрам куба кристаллографической
ячейки. Центр системы координат
параллельны ребрам куба кристаллографической
ячейки. Центр системы координат ![]() находится в центре пластины,
так что ее плоскости соответствуют координатам
находится в центре пластины,
так что ее плоскости соответствуют координатам ![]() .
.
Основная система уравнений движения для нормированных компонент намагниченности имеет вид [30]:
 , (1)
, (1)
а уравнения для ![]() и
и ![]() получаются
циклической перестановкой
получаются
циклической перестановкой ![]() ,
, ![]() ,
, ![]() . Уравнения
для компонент упругого смещения
. Уравнения
для компонент упругого смещения ![]() имеют вид:
имеют вид:
граничные условия:
В работе [20] показано, что поставленную так задачу, в приближении первой упругой моды, можно свести к системе из семи нелинейных дифференциальных уравнений первого порядка без граничных условий. Анализ развития колебаний методом фазового пространства [31-33] требует нахождения координат особых точек, что для такой системы сводится к решению линейного алгебраического уравнения седьмой степени.
Сложность решения поставленной таким образом задачи стимулирует поиск возможностей уменьшения общего числа уравнений, одной из которых является квадратичное приближение по намагниченности, позволяющее свести рассмотрение к более простой системе, состоящей из двух связанных уравнений второго порядка, базирующийся на модели связанных магнитного и упругого осцилляторов.
Приведенная в работах [22,23] такая квадрированная система (с точностью до обозначений) имеет вид:
уравнение для намагниченности:
![]()
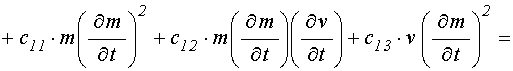
![]() ; (4)
; (4)
уравнение для редуцированного упругого смещения:
![]()
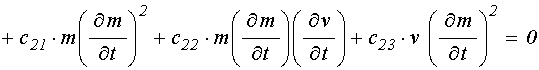 . (5)
. (5)
С учетом обозначения:
входящие в (4)-(5) коэффициенты имеют вид:
![]() ; (7)
; (7)
 ; (8)
; (8)
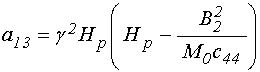 ; (9)
; (9)
 ; (10)
; (10)
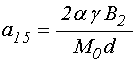 ;
(11)
;
(11)
![]() ; (12)
; (12)
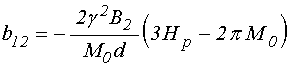 ; (13)
; (13)
 ; (14)
; (14)
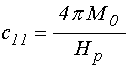 ; (15)
; (15)
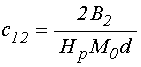 ; (16)
; (16)
 ; (17)
; (17)
![]() ; (18)
; (18)
![]() ; (19)
; (19)
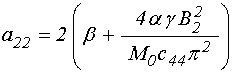 ; (20)
; (20)
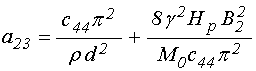 ; (21)
; (21)
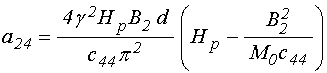 ; (22)
; (22)
 ; (23)
; (23)
 ; (24)
; (24)
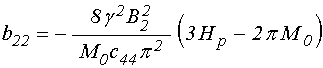 ; (25)
; (25)
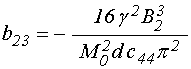 ; (26)
; (26)
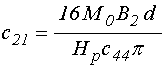 ; (27)
; (27)
 ; (28)
; (28)
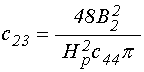 . (29)
. (29)
При этом полное упругое смещение
![]() на поверхностях пластины, выраженное через
редуцированное смещение
на поверхностях пластины, выраженное через
редуцированное смещение ![]() и намагниченность
и намагниченность ![]() , имеет вид:
, имеет вид:
2. Общая модель связанных осцилляторов
Перейдем теперь к модели связанных
осцилляторов в наиболее обобщенном случае, для чего в уравнениях (4)-(5) произведем
замену переменных ![]() ,
, ![]() , а также
возбуждающей силы
, а также
возбуждающей силы ![]() , так что запишем систему
(4)-(5) в виде:
, так что запишем систему
(4)-(5) в виде:
![]()
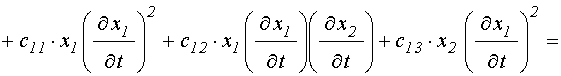
![]() ; (31)
; (31)
![]()
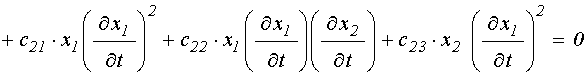 .
(32)
.
(32)
Можно видеть, что такая система
не является полностью симметричной, то есть ее уравнения не переходят одно в другое
при взаимной замене индексов переменных ![]() на
на ![]() и обратно. Симметричными являются только слагаемые
со всеми коэффициентами
и обратно. Симметричными являются только слагаемые
со всеми коэффициентами ![]() , а также с коэффициентами
, а также с коэффициентами
![]() ,
, ![]() и
и ![]() ,
, ![]() соответственно.
Слагаемые с коэффициентами
соответственно.
Слагаемые с коэффициентами ![]() ,
, ![]() , а также со всеми коэффициентами
, а также со всеми коэффициентами ![]() содержат одинаковые степени переменных, друг
в друга не переходящие. Такая несимметричность говорит о несимметричности соответствующего
потенциала, который здесь не является эквивалентным относительно двух своих переменных
содержат одинаковые степени переменных, друг
в друга не переходящие. Такая несимметричность говорит о несимметричности соответствующего
потенциала, который здесь не является эквивалентным относительно двух своих переменных
![]() и
и ![]() . То есть
для получения обобщенной силы для каждого из уравнений надо использовать потенциал
своего собственного вида.
. То есть
для получения обобщенной силы для каждого из уравнений надо использовать потенциал
своего собственного вида.
Такое обстоятельство находится в определенном противоречии с принятым в теоретической механике положением о единстве потенциальной энергии системы в целом, а также о силе, как производной от такой энергии по координате [34-36]. Возможной причиной подобного противоречия, по-видимому, является тот факт, что здесь мы имеем дело не с чисто механической системой, а с системой комбинированной, механика в которой составляет только упругую часть, тогда как другая часть является магнитной. Эта магнитная часть системы подчиняется не механическому уравнению Ньютона второго порядка, а уравнению Ландау-Лифшица, эквивалентному трем уравнениям первого порядка, в результате чего общий порядок системы получается более высоким. Таким образом, квадрированная система (31)-(32) является результатом квадратичного приближения именно такой комбинированной системы, не четвертого (как два уравнения Ньютона), а пятого порядка (как одно уравнение Ньютона плюс одно уравнение Ландау-Лифшица). То есть, несмотря на то, что система (31)-(32) содержит всего два уравнения, что в классическом случае соответствует двум степеням свободы [31-33], она получена на основе полной системы (1)-(3), содержащей пять уравнений первого порядка, что соответствует двум с половиной степеням свободы. Можно предположить, что причиной появления в уравнениях (31)-(32) слагаемых с производными является как раз такая дополнительная половина степени свободы, на которую отличается система (1)-(3) от классической системы двух связанных осцилляторов.
Таким образом, прямое вычисление обобщенной силы путем дифференцирования потенциала по координате здесь не вполне применимо и в какой-то степени может иметь место только для слагаемых, не содержащих производных по времени. В этом случае для каждого из уравнений (31) и (32) должна использоваться своя потенциальная функция, дифференцирование которой по координате может дать обобщенную силу.
Замечание. Вообще говоря, с математической стороны
прием вычисления силы путем дифференцирования потенциала, заданный в трудах классиков
[34-36], является вполне общим. Однако наличие в уравнениях (31)-(32) слагаемых,
содержащих произведения координат на их производные по времени (слагаемые с коэффициентами
![]() ), наводит на мысль о возможности существования
какой-то более общей функции, зависящей не только от координат, как потенциальная
энергия, но и в какой-то степени от производных от координат по времени, то есть
содержащей элементы кинетической энергии. Можно полагать, что построение такой функции
позволило бы обобщить традиционную трактовку Лагранжа, представляющую силу как производную
от потенциальной энергии по координате, то есть ввести в рассмотрение какие-то обобщенные
«силы» более высокого порядка, типа представленных коэффициентами
), наводит на мысль о возможности существования
какой-то более общей функции, зависящей не только от координат, как потенциальная
энергия, но и в какой-то степени от производных от координат по времени, то есть
содержащей элементы кинетической энергии. Можно полагать, что построение такой функции
позволило бы обобщить традиционную трактовку Лагранжа, представляющую силу как производную
от потенциальной энергии по координате, то есть ввести в рассмотрение какие-то обобщенные
«силы» более высокого порядка, типа представленных коэффициентами ![]() в системе (31)-(32). Однако на данный момент
построение такой обобщенной функции можно считать самостоятельной задачей, выходящей
за рамки настоящей работы.
в системе (31)-(32). Однако на данный момент
построение такой обобщенной функции можно считать самостоятельной задачей, выходящей
за рамки настоящей работы.
3. Основные режимы автоколебаний
Основным предметом рассмотрения настоящей работы является выявление наиболее общих условий, при которых в системе возможно существование вынужденных колебаний автомодуляционного характера. Кратко обобщая наиболее характерные свойства описанных в работах [25-29] автомодуляционных колебаний системы двух связанных осцилляторов, можно выделить четыре основных режима.
Режим №1 – регулярные колебания без какой-либо модуляции (синусоидальные). При включении возбуждающей силы после небольшого периода установления, определяемого временем релаксации осцилляторов, колебания приобретают четко выраженный регулярный синусоидальный характер с постоянной амплитудой и постоянным периодом, равным периоду возбуждения.
Режим №2 – регулярные колебания с модуляцией амплитуды (автомодулированные). После первичной релаксации колебания приобретают регулярный периодический характер, однако амплитуда колебаний в пределах каждого периода меняется по определенному единому для всех периодов закону, то есть имеет место регулярная автомодуляция колебаний. Период таких автомодулированных колебаний превышает период возбуждения в два или большее, в том числе, возможно, дробное число раз, однако в установившемся режиме сохраняется строго постоянным.
Режим №3 – нерегулярные колебания с ограниченной амплитудой и квазислучайной модуляцией (квазистохастические). Начиная с момента включения возбуждающей силы колебания приобретают резко нерегулярный квазихаотический характер, так что амплитуда и длительность отдельного колебания меняются случайным образом. Максимальная амплитуда является ограниченной, однако в пределах такого ограничения меняется произвольно. Следы периодичности во времени, соответствующей возбуждающей силе, в какой-то степени сохраняются, однако могут нарушаются в обе стороны в два и более раз.
Режим №4 – колебания с неограниченно нарастающей амплитудой (уход системы на бесконечность). Начиная с момента включения возбуждающей силы размах колебаний увеличивается, после чего, достигая определенного предела, устремляется к бесконечности. Этот режим может явиться как развитие во времени любых колебаний из первых трех режимов, а также может быть апериодическим, то есть система может уходить на бесконечность сразу после включения возбуждения, без предварительных переколебаний.
Рассмотрим вкратце, какую роль в формировании перечисленных режимов играют слагаемые, составляющие уравнения (31)-(32).
4. Роль отдельных слагаемых связанных уравнений
В уравнениях (31)-(32), кроме
основных первых двух слагаемых, описывающих ускорение движения осциллятора и затухание
этого движения, присутствуют слагаемые двух видов. Слагаемые первого вида содержат
только ту же переменную, что и первые два слагаемых, то есть в уравнении (31) –
переменную ![]() , в уравнении (32) – переменную
, в уравнении (32) – переменную ![]() . Слагаемые второго вида – или другую переменную,
или обе, то есть в уравнении (31) – переменную
. Слагаемые второго вида – или другую переменную,
или обе, то есть в уравнении (31) – переменную ![]() или обе
переменные
или обе
переменные ![]() и
и ![]() , в уравнении
(32) – переменную
, в уравнении
(32) – переменную ![]() или также обе переменные
или также обе переменные ![]() и
и ![]() . При этом
слагаемые первого вида обеспечивают нелинейность того осциллятора, к которому они
принадлежат, а второго – связь между обоими осцилляторами.
. При этом
слагаемые первого вида обеспечивают нелинейность того осциллятора, к которому они
принадлежат, а второго – связь между обоими осцилляторами.
Рассмотрим роль упомянутых слагаемых в формировании ухода системы на бесконечность.
В работах [21,24] показано, что уход на бесконечность линеаризованной системы с производными эквивалентен переориентации по полной системе. При этом причиной ухода на бесконечность являются слагаемые с производными, которые обеспечивают компенсацию затухания, то есть как бы отрицательную добавку к сопротивлению, будучи слагаемыми той же структуры. При этом связь через сами переменные не может обеспечить ухода на бесконечность, так как является линейной и приводит только к изменению частоты, как слагаемые той же структуры, но «перекрестные» в обоих уравнениях.
В этих работах для случая свободных колебаний получен аналитический критерий постоянства амплитуды колебаний при связи через производные, представляющий собой комбинацию из параметров уравнений осцилляторов. При недостижении этого критерия свободные колебания системы во времени затухают. При точном выполнении критерия их амплитуда во времени остается постоянной. При превышении критерия амплитуда колебаний экспоненциально нарастает, то есть система уходит на бесконечность.
В работе [30] показано, что в системе без производных наличие квадратичной связи в первом уравнении также может обеспечить уход на бесконечность – благодаря кубичности потенциала.
Итак, в основе ухода на бесконечность могут лежать два принципиально различающихся механизма:
1) главная связь – через производные, линейная в обоих уравнениях, возможная дополнительная – через переменные, также линейная;
2) главная связь – через переменные, квадратичная в первом уравнении и линейная во втором, возможная дополнительная – через производные, линейная в обоих уравнениях.
Первый из этих механизмов может быть интерпретирован на основе модели отрицательного сопротивления, второй – на основе модели потенциала.
В работах [22, 27] показано, что уход линейной системы на бесконечность для случая линейной связи через производные и линейной через переменные (первый вид связи), может быть скомпенсирован кубической нелинейностью по переменной в первом уравнении. В работе [30] показано, что уход системы на бесконечность для случая связи по переменным, квадратичной в первом уравнении и линейной во втором (второй вид связи) также может быть скомпенсирован кубической нелинейностью по переменной в первом уравнении. Таким образом, кубическая нелинейность в первом уравнении является универсальным средством компенсации ухода на бесконечность. Это происходит благодаря квадратичности потенциала, обеспечивающего требуемую кубическую нелинейность в первом уравнении.
Можно полагать, что и более высокие четные степени потенциала (по одной только первой переменной без второй), обеспечивающие нечетную нелинейность в первом уравнении, также должны приводить к компенсации ухода системы на бесконечность.
В качестве критерия возможности ухода системы на бесконечность за счет потенциала можно предложить наглядную геометрическую интерпретацию. При этом зависимость потенциала от переменной изображается параболой с двумя ветвями, при положительных коэффициентах которой четные степени при увеличении абсолютной величины переменной обеспечивают стремление обеих ветвей к плюс бесконечности, а нечетные – стремление положительной ветви к плюс бесконечности, а отрицательной – к минус бесконечности. Такое стремление отрицательной ветви к минус бесконечности и обеспечивает уход системы на бесконечность как стремление к минимуму потенциальной энергии.
Модель потенциала позволяет интерпретировать уход системы на бесконечность и его компенсацию для случая связи уравнений через переменные. Для связи через производные модель потенциала непригодна, так как, согласно определению, потенциал зависеть от времени не должен. В этом случае потенциал – как бы уровень максимальной потенциальной энергии системы, от времени не зависящий.
5. Полная система на основе потенциала
Из рассмотрения результатов работ [25-29] можно видеть, что за счет связи, как через производные, так и через переменные, получается значительное разнообразие видов автомодуляционных колебаний, укладывающихся в рамки схематичной классификации, приведенной в разделе №3.
В качестве первого наиболее простого шага, в настоящей работе ограничимся рассмотрением связи только через переменные, то есть в уравнениях (31)-(32) слагаемые, содержащие производные, опускаем. В результате система (31)-(32) принимает вид:
![]() ; (33)
; (33)
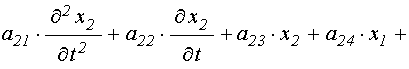
![]() . (34)
. (34)
Введем обобщенные потенциалы, которые, согласно показанному в разделе №2, для каждого осциллятора должны быть различными:
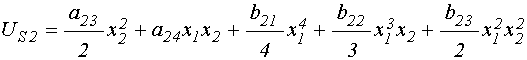 . (36)
. (36)
Следуя определению обобщенных сил, как производных от потенциала по координате:
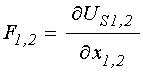 , (37)
, (37)
получаем эти силы в виде:
![]() ; (38)
; (38)
![]() .(39)
.(39)
При этом уравнения (33)-(34) принимают вид:
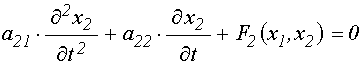 ; (41)
; (41)
Заметим, что в классическом
определении обобщенной силы [34-36] перед дробью присутствует знак минус. Однако
и в уравнениях (40)-(41) перед слагаемыми, содержащими ![]() также
должен быть минус. Поэтому здесь, чтобы избежать умножения минуса на минус, в обоих
случаях взят плюс.
также
должен быть минус. Поэтому здесь, чтобы избежать умножения минуса на минус, в обоих
случаях взят плюс.
Потенциалы в виде (35)-(36) содержат слагаемые только четных степеней – второй и четвертой. Согласно работе [30], слагаемые второй степени могут обеспечить только линейную связь между осцилляторами. При достаточной величине такой связи возможен уход системы на бесконечность, как это следует из загибов вниз диаметрально противоположных углов потенциальной поверхности на рис.5в,д в работе [30]. Однако слагаемые четвертой степени не могут обеспечить уход системы на бесконечность, так как при этом все края потенциальной поверхности загибаются вверх, как это показано на рис.5г в той же работе. С другой стороны, слагаемые третьей степени в определенном интервале своих величин также могут обеспечить уход системы на бесконечность за счет загиба вниз углов потенциальной поверхности одинакового знака, как это видно там же из рис.5е.
Поэтому для полноты картины потенциалы (35)-(36) следует дополнить слагаемыми третьей степени, в результате чего они принимают вид:
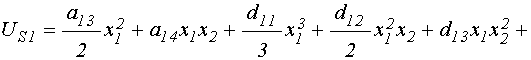
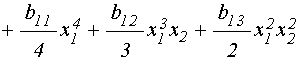 ; (42)
; (42)
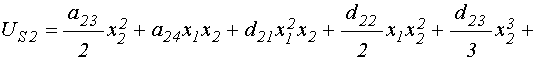
 . (43)
. (43)
При этом силы получаются в виде:
![]()
![]() ; (44)
; (44)
![]()
![]() , (45)
, (45)
а развернутые уравнения принимают вид:
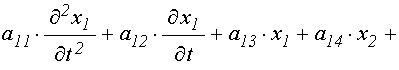
![]()
![]() ; (46)
; (46)
![]()
![]() . (47)
. (47)
Можно полагать, что такая система содержит в себе все возможные варианты формирования автомодуляционных режимов колебаний за счет связи через переменные при условии потенциала не выше четвертой степени.
6. Роль квадратичности связи первого осциллятора
Предложенная в предыдущем разделе система (46)-(47) является для анализа весьма сложной, поэтому сначала рассмотрим более простые ее частные случаи, достаточные для формирования колебаний автомодуляционного характера, укладывающихся в классификацию, приведенную в разделе №3.
По-видимому, один из самых простых видов автомодуляционных колебаний описан в работе [30]. При этом связь первого осциллятора со вторым является квадратичной, а второго с первым – линейной, то есть связанные уравнения имеют вид:
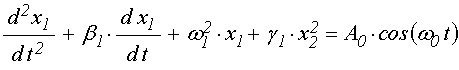 ; (48)
; (48)
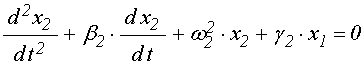 . (49)
. (49)
Здесь ![]() ,
, ![]() ,
, ![]() – координатные
переменные, параметры затухания и собственные частоты осцилляторов,
– координатные
переменные, параметры затухания и собственные частоты осцилляторов, ![]() – коэффициенты связи,
– коэффициенты связи, ![]() и
и ![]() – амплитуда
и частота возбуждающей силы.
– амплитуда
и частота возбуждающей силы.
Легко видеть, что такая система
является частным случаем системы (47)-(48) при ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , а все остальные коэффициенты равны нулю.
, а все остальные коэффициенты равны нулю.
Рассмотрим здесь роль квадратичности
связи первого осциллятора более подробно, для чего обратимся к рис.2, где проведено
сравнение случая квадратичной связи со случаем линейной. Для исключения влияния
других факторов возьмем параметры обоих осцилляторов одинаковыми, то есть положим
![]() ,
, ![]() , а также
собственные частоты обоих осцилляторов и частоту возбуждения также между собой равными:
, а также
собственные частоты обоих осцилляторов и частоту возбуждения также между собой равными:
![]() .
.
Рис.2а соответствует линейной
связи между обоими осцилляторами. Видно, что в этом случае колебания обоих осцилляторов
являются регулярными, практически синусоидальными. Колебания второго осциллятора
полностью подобны колебаниям первого (с точностью до множителя ![]() ), причем отстают по фазе от колебаний первого
на
), причем отстают по фазе от колебаний первого
на ![]() . Соответствующий параметрический портрет
(рис.2б) имеет вид правильного эллиптического кольца с узкой образующей. Легкая
сплюснутость по вертикали обусловлена меньшей амплитудой колебаний второго осциллятора
по сравнению с амплитудой первого (около
. Соответствующий параметрический портрет
(рис.2б) имеет вид правильного эллиптического кольца с узкой образующей. Легкая
сплюснутость по вертикали обусловлена меньшей амплитудой колебаний второго осциллятора
по сравнению с амплитудой первого (около ![]() ).
).
Рис.2в соответствует квадратичной
связи первого осциллятора относительно второго при сохранении линейности второго
относительно первого. Видно, что в этом случае колебания осцилляторов также сохраняют
определенную регулярность, однако амплитуда через каждое колебание меняется, причем
минимальный размах от максимального для первого осциллятора составляет около ![]() , а для второго – около
, а для второго – около ![]() (в работе [30] такое чередование амплитуды
названо «расщеплением»).
(в работе [30] такое чередование амплитуды
названо «расщеплением»).
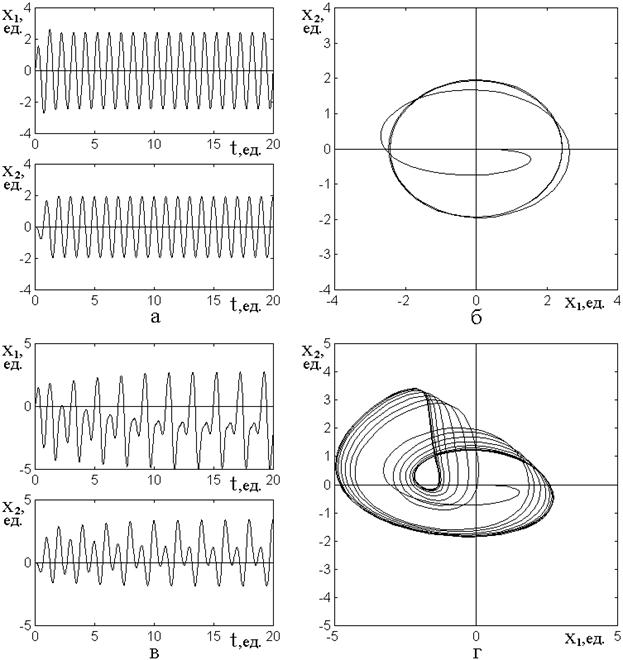
Рис.2. Развитие колебаний осцилляторов во времени (а,в) и соответствующие параметрические портреты (б,г) при различных видах связи.
а,б – связь линейная по обоим осцилляторам;
в,г – связь квадратичная по первому и линейная по второму осциллятору.
Параметры: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Можно видеть, что благодаря
такому чередованию амплитуд период результирующего колебания удваивается. Колебания
второго осциллятора по-прежнему отстают по фазе от колебаний первого на ![]() , однако теперь амплитуды чередующихся колебаний
находятся в противофазе. Соответствующий параметрический портрет (рис.2г) имеет
вид вложенных друг в друга почти круговых циклов, однако раздвинутых друг от друга,
так что в области перекрытия образуется петля. Следующие друг за другом траектории
слегка относительно смещаются, в результате чего образующая приобретает некоторое
расщепление.
, однако теперь амплитуды чередующихся колебаний
находятся в противофазе. Соответствующий параметрический портрет (рис.2г) имеет
вид вложенных друг в друга почти круговых циклов, однако раздвинутых друг от друга,
так что в области перекрытия образуется петля. Следующие друг за другом траектории
слегка относительно смещаются, в результате чего образующая приобретает некоторое
расщепление.
Из рассмотрения рис.2 можно видеть, что колебания второго осциллятора в обоих случаях довольно подобным образом повторяют колебания первого, причем такая характерная особенность, как чередование амплитуды с удвоением периода обусловлено именно квадратичностью связи первого осциллятора относительно второго.
Движение первого осциллятора, находящегося под непосредственным действием возбуждающей силы, можно приближенно представить таким образом, что его колебания через связь со вторым возбуждают вынужденные колебания второго, после чего возвращаются к нему же через связь второго с первым. То есть относительно первого осциллятора имеет место «двухступенчатая» связь, которую для него можно рассматривать как определенное самовоздействие. В случае линейной связи в обоих осцилляторах такое самовоздействие, оставаясь линейным, общего характера колебаний не меняет. В случае квадратичной связи за счет ее нелинейности появляются комбинационные частоты, которые и приводят к чередованию амплитуды колебаний с удвоением периода.
Подобное поведение колебаний в случае квадратичной связи первого осциллятора отмечалось в работе [30]. Там же показано, что наблюдаемый двухамплитудный вид колебаний можно представить с помощью эмпирической зависимости, состоящей из суммы двух синусоид, частота одной из которых равна частоте возбуждения, а частота второй – превышает первую в два раза. В этом случае появление в спектре колебаний второй синусоиды можно приписать именно нелинейности связи.
Замечание. Контрольная проверка показывает, что в случае квадратичной связи в обоих осцилляторах, их колебания регуляризуются, приобретая вид, подобный показанному на рис.2а. Параметрический потрет при этом приобретает вид треугольника с сильно закругленными углами. Можно полагать, что такая регуляризация колебаний обусловлена симметрией системы, а совокупная нелинейность обоих осцилляторов проявляется в искажении формы параметрического портрета, делая ее отличной от круговой.
7. Осциллятор с квадратичной нелинейностью. Свободные колебания
В разделе №6 показано, что колебания второго осциллятора, в основном, повторяют колебания первого. При этом роль второго осциллятора сводится, как бы к «возвращению» колебаний первого осциллятора ему же с учетом возведения в квадрат. Поэтому в качестве наиболее простой модели автомодуляции колебаний можно рассмотреть единственный возбуждаемый внешней силой первый осциллятор, содержащий квадратичную нелинейность, определяемую соответствующим потенциалом третьего порядка.
Будем исходить из общего уравнения для свободных колебаний одного осциллятора:
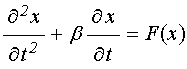 , (50)
, (50)
где ![]() – обобщенная
сила, являющаяся производной от потенциала по координате с обратным знаком:
– обобщенная
сила, являющаяся производной от потенциала по координате с обратным знаком:
 . (51)
. (51)
Пусть потенциал является кубическим, то есть имеет вид:
Сила (51) равна:
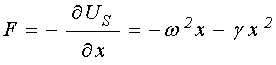 . (53)
. (53)
Уравнение для свободных колебаний (50) принимает вид:
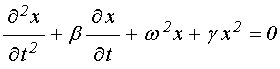 . (54)
. (54)
Для исследования этого уравнения обратим к рис.3.
Рис.3. Потенциал (а) и развитие свободных колебаний во времени (б) для одного осциллятора с квадратичной нелинейностью.
Параметры: ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
На рис.3а показана зависимость
потенциала ![]() от координаты
от координаты ![]() , построенная
по формуле (52). Видно, что потенциал представляет собой кубическую параболу с минимумом
в точке Е. Максимум на левой ветви отмечен точкой А, уровень потенциала, соответствующий
этому максимуму, показан горизонтальной пунктирной линией, пересечение которой с
провой ветвью параболы отмечено точкой В. Периодические колебания возможны только
в пределах потенциальной ямы между А и В, то есть при уровне потенциала между пунктирной
линией АВ и минимумом Е. При начальном уровне потенциала вне этой области, то есть
при
, построенная
по формуле (52). Видно, что потенциал представляет собой кубическую параболу с минимумом
в точке Е. Максимум на левой ветви отмечен точкой А, уровень потенциала, соответствующий
этому максимуму, показан горизонтальной пунктирной линией, пересечение которой с
провой ветвью параболы отмечено точкой В. Периодические колебания возможны только
в пределах потенциальной ямы между А и В, то есть при уровне потенциала между пунктирной
линией АВ и минимумом Е. При начальном уровне потенциала вне этой области, то есть
при ![]() или
или ![]() система
уходит на бесконечность по левой спадающей ветви параболы. Для удобства рисунка
значение
система
уходит на бесконечность по левой спадающей ветви параболы. Для удобства рисунка
значение ![]() задано числено равным
задано числено равным ![]() . Удобство состоит в том, что при таком выборе
потенциальная яма ограничена пределами: точка А –
. Удобство состоит в том, что при таком выборе
потенциальная яма ограничена пределами: точка А – ![]() , точка
В –
, точка
В – ![]() , то есть небольшими легко узнаваемыми целыми
числами.
, то есть небольшими легко узнаваемыми целыми
числами.
На рис.3б показано развитие
свободных колебаний осциллятора во времени внутри потенциальной ямы. Вверху – начиная
с точки А, внизу – с точки В (начальные уровни показаны укрупненными точками). Видно,
что в обоих случаях колебания представляют собой синусоиды, затухающие с одной и
той же постоянной времени. На верхнем рисунке колебания начинают развиваться с небольшой
задержкой во времени (около ![]() ), что связано с малостью
производной потенциала по координате вблизи точки А. В обоих случаях колебания сдвинуты
вниз относительно оси
), что связано с малостью
производной потенциала по координате вблизи точки А. В обоих случаях колебания сдвинуты
вниз относительно оси ![]() , что обусловлено некоторой несимметричностью
потенциальной ямы.
, что обусловлено некоторой несимметричностью
потенциальной ямы.
8. Осциллятор с квадратичной нелинейностью. Вынужденные колебания
Рассмотрим теперь вынужденные колебания того же осциллятора под действием синусоидальной силы. Соответствующее уравнение колебаний имеет вид:
Обратимся к рис.4, где показаны
развертки во времени колебаний осциллятора, описываемых уравнением (55), при различной
степени возбуждения. Частота возбуждения ![]() принята
равной собственной частоте свободного осциллятора
принята
равной собственной частоте свободного осциллятора ![]() . Параметр
затухания выбран несколько большим, чем на рис.3, что сделано для наглядности рисунка,
чтобы исключить влияние биений, возникающих в первый момент после включении возбуждения.
. Параметр
затухания выбран несколько большим, чем на рис.3, что сделано для наглядности рисунка,
чтобы исключить влияние биений, возникающих в первый момент после включении возбуждения.
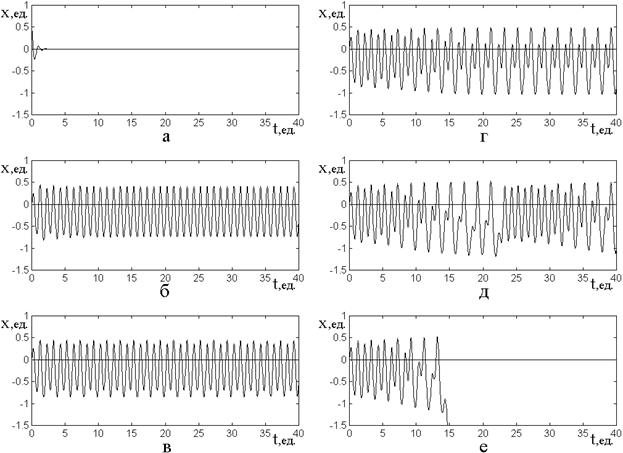
Рис.4. Вынужденные колебания осциллятора с квадратичной нелинейностью при различной степени возбуждения.
а – ![]() ; б –
; б –
![]() ; в –
; в – ![]() ;
;
г – ![]() ; д –
; д –
![]() ; е –
; е – ![]()
Параметр затухания ![]() , остальные параметры – те же, что на рис.3.
, остальные параметры – те же, что на рис.3.
Рис.4а соответствует свободным
колебания при начальном отклонении ![]() Видно, что при выбранном
параметре затухания амплитуда таких колебаний спадает практически до нуля при времени
порядка
Видно, что при выбранном
параметре затухания амплитуда таких колебаний спадает практически до нуля при времени
порядка ![]()
Рис.4б соответствует колебаниям
при умеренном уровне возбуждения, то есть таком, когда координата осциллятора в
процессе колебаний заметно не доходит до краев ямы, в данном случае – примерно на
![]() от своей полной амплитуды. Можно видеть, что
в этом случае колебания являются полностью регулярными, близкими к синусоидальным.
Амплитуда их постоянна, частота совпадает с частотой возбуждения. Некоторое смещение
вниз (на
от своей полной амплитуды. Можно видеть, что
в этом случае колебания являются полностью регулярными, близкими к синусоидальным.
Амплитуда их постоянна, частота совпадает с частотой возбуждения. Некоторое смещение
вниз (на ![]() ) обусловлено асимметричностью потенциальной
ямы.
) обусловлено асимметричностью потенциальной
ямы.
Рис.4в соответствует несколько
большему уровню возбуждения, при котором значение координаты осциллятора приближается
к краям ямы до уровня порядка ![]() от полной амплитуды. Колебания
остаются полностью регулярными, однако амплитуда их через одно колебание принимает
большее или меньшее значение, то есть меняется в ту и другую сторону приблизительно
на
от полной амплитуды. Колебания
остаются полностью регулярными, однако амплитуда их через одно колебание принимает
большее или меньшее значение, то есть меняется в ту и другую сторону приблизительно
на ![]() , что приводит к увеличению периода в два раза.
Такие колебания будем далее называть «двухамплитудными с удвоенным периодом» (в
работе [30] подобное чередование амплитуды названо «расщеплением»). Численная проверка,
подобная проведенной в разделе №10 работы [30], показывает, что такие колебания
по форме могут быть довольно близко представлены в виде суммы двух синусоид, частота
одной из которых равна частоте возбуждения, а вторая превышает ее в два раза. То
есть основная синусоида как бы модулируется двойной частотой, причем в рассматриваемом
здесь случае глубина модуляции невелика и составляет около
, что приводит к увеличению периода в два раза.
Такие колебания будем далее называть «двухамплитудными с удвоенным периодом» (в
работе [30] подобное чередование амплитуды названо «расщеплением»). Численная проверка,
подобная проведенной в разделе №10 работы [30], показывает, что такие колебания
по форме могут быть довольно близко представлены в виде суммы двух синусоид, частота
одной из которых равна частоте возбуждения, а вторая превышает ее в два раза. То
есть основная синусоида как бы модулируется двойной частотой, причем в рассматриваемом
здесь случае глубина модуляции невелика и составляет около ![]() .
.
Рис.4г соответствует еще более
высокому уровню возбуждения, при котором координата колеблющегося осциллятора приближается
к краям ямы до уровня порядка ![]() . Колебания сохраняют определенную
регулярность и двухамплитудный модулированный вид с удвоенным периодом, однако теперь
глубина модуляции сначала небольшая, не более
. Колебания сохраняют определенную
регулярность и двухамплитудный модулированный вид с удвоенным периодом, однако теперь
глубина модуляции сначала небольшая, не более ![]() , постепенно
увеличивается, достигая при времени около
, постепенно
увеличивается, достигая при времени около ![]() уровня
уровня
![]() , после чего не меняется. То есть глубина модуляции
претерпевает определенное «установление» с характерным временем
, после чего не меняется. То есть глубина модуляции
претерпевает определенное «установление» с характерным временем ![]()
Рис.4д соответствует столь
высокому уровню возбуждения, что координата колеблющегося осциллятора приближается
к краям ямы на ![]() . Колебания в значительной степени
утрачивают регулярность, однако их двухамплитудный двухпериодический характер, в
основном, сохраняется. Наблюдается ярко выраженная «вторичная модуляция», представляющая
собой периодическое изменение глубины двухамплитудной модуляции от
. Колебания в значительной степени
утрачивают регулярность, однако их двухамплитудный двухпериодический характер, в
основном, сохраняется. Наблюдается ярко выраженная «вторичная модуляция», представляющая
собой периодическое изменение глубины двухамплитудной модуляции от ![]() до
до ![]() . Период
такой вторичной модуляции составляет около
. Период
такой вторичной модуляции составляет около ![]()
Рис.4е соответствует настолько
высокому уровню возбуждения, что колебания осциллятора приближаются к краям ямы
практически вплотную. Благодаря небольшим флуктуациям амплитуды, в некоторый момент
времени координата осциллятора может перевалить через потенциальный барьер (точка
А на рис.3а), в результате чего происходит «разнос» системы и она уходит на минус
бесконечность. В данном случае это происходит при времени около ![]()
Таким образом, можно видеть,
что единственный осциллятор с квадратичной нелинейностью, будучи возбужденным на
собственной частоте, может обеспечить довольно разнообразные виды автомодулированных
колебаний, в том числе двухамплитудные с удвоением периода, с установлением, со
вторичной модуляцией, а также уход системы на бесконечность. Все такие автомодуляционные
колебания наблюдаются при уровне возбуждения, приближающемся к краям потенциальной
ямы (не далее ![]() от центра). Следует отметить, что
по мере увеличения уровня возбуждения различные виды колебаний переходят друг в
друга плавно, то есть беспороговым образом, кроме ухода системы на бесконечность,
порог которого является весьма резким (менее
от центра). Следует отметить, что
по мере увеличения уровня возбуждения различные виды колебаний переходят друг в
друга плавно, то есть беспороговым образом, кроме ухода системы на бесконечность,
порог которого является весьма резким (менее ![]() ).
).
Предварительная проверка показывает, что при отстройке частоты возбуждения от собственной могут наблюдаться еще более сложные виды автомодуляционных колебаний, однако на данном этапе их рассмотрение выходит за рамки настоящей работы.
9. Сравнение с уравнением Дуффинга
Уравнение (55) можно считать по форме в какой-то степени родственным уравнению Дуффинга [32]:
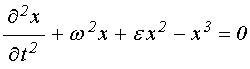 . (56)
. (56)
Частный случай такого уравнения при ![]() рассмотрен в [32] на стр.299-304. При этом
принципиально важным становится последнее слагаемое, содержащее
рассмотрен в [32] на стр.299-304. При этом
принципиально важным становится последнее слагаемое, содержащее ![]() , соответствующее потенциалу четвертого порядка
с отрицательным знаком. Потенциал такого вида представляет собой параболу четвертой
степени, обе ветви которой уходят на минус бесконечность. То есть потенциал представляет
собой квадратичную яму (за счет слагаемого, содержащего
, соответствующее потенциалу четвертого порядка
с отрицательным знаком. Потенциал такого вида представляет собой параболу четвертой
степени, обе ветви которой уходят на минус бесконечность. То есть потенциал представляет
собой квадратичную яму (за счет слагаемого, содержащего ![]() ),
окруженную двумя барьерами, по внешние стороны от которых он спадет вниз бесконечным
образом.
),
окруженную двумя барьерами, по внешние стороны от которых он спадет вниз бесконечным
образом.
Отличие рассматриваемого здесь
случая (55) состоит в том, что потенциал имеет лишь один такой барьер, а на месте
другого – подъем, возрастающий к плюс бесконечности. Таким образом, потенциальная
яма является несимметричной, что существенно отражается на форме колебаний. Дополнительным
отличием уравнения (55) является рассмотрение затухания, обеспечиваемого вторым
слагаемым, содержащим параметр ![]() . В отличие от уравнения
Дуффинга, решаемого в [32] для свободных колебаний системы, рассматриваемый здесь
случай (55) относится именно к вынужденным колебаниям, причем для удобства рассмотрения
параметр затухания положен столь большим, что собственные колебания значительной
роли не играют (рис.4а).
. В отличие от уравнения
Дуффинга, решаемого в [32] для свободных колебаний системы, рассматриваемый здесь
случай (55) относится именно к вынужденным колебаниям, причем для удобства рассмотрения
параметр затухания положен столь большим, что собственные колебания значительной
роли не играют (рис.4а).
10. Модель фазовой задержки
В предыдущем разделе показано, что при достаточно высоком уровне возбуждения, приближающемся к уходу системы на бесконечность, вынужденные колебания приобретают двухамплитудный характер, сопровождающийся удвоением периода. Там же было выявлено, что причиной подобной трансформации колебаний является квадратичная нелинейность первого осциллятора, обусловленная его кубическим потенциалом. Рассмотрим теперь механизм такой трансформации колебаний более подробно.
Сначала обратимся к колебаниям осциллятора в случае ненулевого начального отклонения, для чего рассмотрим рис.5, где показано развитие процесса таких колебаний во времени.
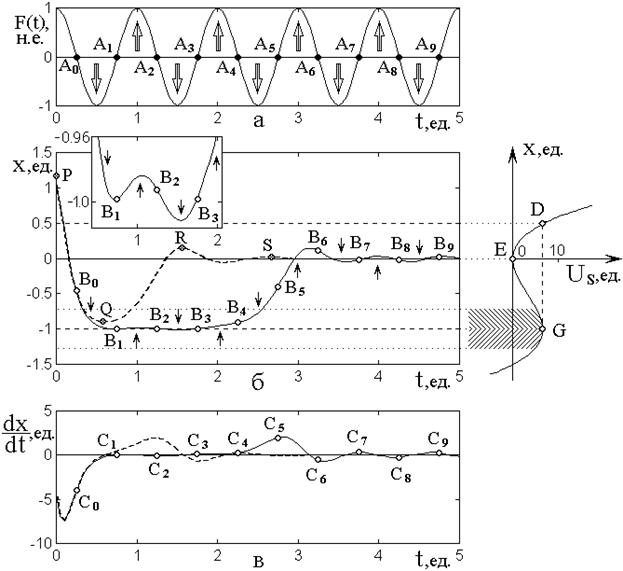
Рис.5. Колебания осциллятора с квадратичной нелинейностью.
а – вынуждающая сила, развитее во времени;
б – смещение осциллятора во времени: колебания
свободные (пунктир) и вынужденные (сплошная линия); справа – зависимость потенциала
от координаты осциллятора, штриховкой показана окрестность потенциального барьера;
горизонтальные пунктирные и точечные линии – значения координаты, соответствующие
характерным уровням потенциала; на врезке – участок кривой между ![]() и
и ![]() в крупном
масштабе;
в крупном
масштабе;
в – скорость движения осциллятора во времени: колебания свободные (пунктир) и вынужденные (сплошная линия).
Точки ![]() ,
, ![]()
![]() – характерные позиции вынуждающей
силы, смещения и скорости.
– характерные позиции вынуждающей
силы, смещения и скорости.
Параметры: ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Рис.5а соответствует развертке
во времени вынуждающей силы ![]() . Для удобства чертежа
эта сила нормирована на единицу, для чего ее амплитуда умножена на
. Для удобства чертежа
эта сила нормирована на единицу, для чего ее амплитуда умножена на ![]() . Точки
. Точки ![]() соответствуют
последовательному прохождению силы через нуль. Стрелками показано направление воздействия
этой силы на осциллятор: стрелки вверх означают, что сила действует в положительном
направлении оси
соответствуют
последовательному прохождению силы через нуль. Стрелками показано направление воздействия
этой силы на осциллятор: стрелки вверх означают, что сила действует в положительном
направлении оси ![]() , стрелки вниз – в отрицательном.
Это рисунок является вспомогательным и помещен здесь для наглядности пояснения развития
процесса колебаний во времени
, стрелки вниз – в отрицательном.
Это рисунок является вспомогательным и помещен здесь для наглядности пояснения развития
процесса колебаний во времени
На рис.5б и 5в показано собственно
смещение осциллятора во времени и соответствующая этому смещению скорость его движения.
Будем полагать, что в начальный момент времени задано начальное смещение осциллятора
– точка Р, в которой смещение равно ![]() . Для сравнения пунктиром
показано развитие колебаний в отсутствие вынуждающей силы. При этом осциллятор движется
по кривой PQRS, затухание которой обусловлено значительной величиной параметра
. Для сравнения пунктиром
показано развитие колебаний в отсутствие вынуждающей силы. При этом осциллятор движется
по кривой PQRS, затухание которой обусловлено значительной величиной параметра ![]() . После первого переколебания между точками
P и Q, осциллятор выходит на точку R, приходящуюся на минимум потенциала, после
чего совершает сильно затухающие колебания с периодом порядка QR, соответствующим
его собственной частоте.
. После первого переколебания между точками
P и Q, осциллятор выходит на точку R, приходящуюся на минимум потенциала, после
чего совершает сильно затухающие колебания с периодом порядка QR, соответствующим
его собственной частоте.
Скорость (рис.5в) по мере
приближения осциллятора к точке Q (рис.5б) падает до нуля, что связано с выходом
потенциала на горизонтальную касательную вблизи вершины потенциального барьера.
Как раз в этом месте направление движения осциллятора меняется на противоположное
(происходит «поворот»), в результате чего скорость, пройдя через нуль вблизи точки
![]() , меняет знак, после чего, пройдя через небольшой
максимум в районе
, меняет знак, после чего, пройдя через небольшой
максимум в районе ![]() , снова стремится к нулю вблизи точки
, снова стремится к нулю вблизи точки
![]() и далее совершает затухающие колебания, соответствующие
стремлению осциллятора к успокоению на дне потенциальной ямы.
и далее совершает затухающие колебания, соответствующие
стремлению осциллятора к успокоению на дне потенциальной ямы.
Важным фактором является то
обстоятельство, что вблизи точки Q (рис.5б) осциллятор находится вблизи вершины
потенциального барьера, вследствие чего сила, скатывающая его в яму, значительно
уменьшается. Поэтому вблизи этой точки скорость движения осциллятора заметно уменьшается
и время выхода из этой области до точки R получается значительно большим половины
периода собственных колебаний осциллятора. То есть осциллятор в своем движении как
бы задерживается по фазе на определенный промежуток времени ![]() , обусловленный пологим характером зависимости
потенциала от координаты вблизи барьера – между точками G и E, особенно вблизи точки
G. Заметим, что на другой стороне потенциальной ямы между точками E и D спад потенциала
значительно более крутой, поэтому задержка осциллятора в своем движении там не имеет
места.
, обусловленный пологим характером зависимости
потенциала от координаты вблизи барьера – между точками G и E, особенно вблизи точки
G. Заметим, что на другой стороне потенциальной ямы между точками E и D спад потенциала
значительно более крутой, поэтому задержка осциллятора в своем движении там не имеет
места.
При наличии вынуждающей силы
(сплошная кривая) характер колебаний сильно меняется. Между точками ![]() и
и ![]() направление
действия силы (показано стрелкой вниз) совпадает с направлением собственного движения
осциллятора прочь от дна потенциальной ямы, однако между точками
направление
действия силы (показано стрелкой вниз) совпадает с направлением собственного движения
осциллятора прочь от дна потенциальной ямы, однако между точками ![]() и
и ![]() направление
действия силы меняется на противоположное (стрелка вверх), снова сталкивая осциллятор
в яму. Однако такое действие силы продолжается недолго. Осциллятор, вследствие малости
своей скорости в окрестности точки
направление
действия силы меняется на противоположное (стрелка вверх), снова сталкивая осциллятор
в яму. Однако такое действие силы продолжается недолго. Осциллятор, вследствие малости
своей скорости в окрестности точки ![]() (соответствующей близкой
к нулю точке
(соответствующей близкой
к нулю точке ![]() на рис.5в), еще не успевает приблизиться к
минимуму потенциала (точка E), как между точками
на рис.5в), еще не успевает приблизиться к
минимуму потенциала (точка E), как между точками ![]() и
и ![]() сила снова действует опять в положительном
направлении оси
сила снова действует опять в положительном
направлении оси ![]() (стрелка вниз), в результате чего
движение осциллятора к минимуму потенциала замедляется. То есть направление действия
силы на противоположное меняется за промежуток времени значительно меньший времени
задержки осциллятора в окрестности пологого склона потенциального барьера. Такое
перемежающееся действие вынуждающей силы («туда-сюда») приводит к значительному
увеличению задержки осциллятора на стороне ямы, соответствующей барьеру, в результате
чего осциллятор приближается к дну ямы только между точками
(стрелка вниз), в результате чего
движение осциллятора к минимуму потенциала замедляется. То есть направление действия
силы на противоположное меняется за промежуток времени значительно меньший времени
задержки осциллятора в окрестности пологого склона потенциального барьера. Такое
перемежающееся действие вынуждающей силы («туда-сюда») приводит к значительному
увеличению задержки осциллятора на стороне ямы, соответствующей барьеру, в результате
чего осциллятор приближается к дну ямы только между точками ![]() и
и ![]() при времени
порядка
при времени
порядка ![]() Можно видеть, что это время значительно (более
чем в два раза) превышает время задержки при свободных колебаниях осциллятора (то
есть
Можно видеть, что это время значительно (более
чем в два раза) превышает время задержки при свободных колебаниях осциллятора (то
есть ![]() ), что можно объяснить периодической подкачкой
энергии к осциллятору за счет действия вынуждающей силы.
), что можно объяснить периодической подкачкой
энергии к осциллятору за счет действия вынуждающей силы.
11. Модель двухамплитудных колебаний
Проделанное рассмотрение относится
к случаю сравнительно небольшой амплитуды возбуждающей силы. При этом в установившемся
режиме колебания происходят в небольшой окрестности дна потенциальной ямы. Так из
рис.5б можно видеть, что в установившемся режиме, то есть при времени больше ![]() , амплитуда колебаний составляет около
, амплитуда колебаний составляет около ![]() , что намного меньше амплитуды, требуемой для
достижения потенциального барьера в точке G (
, что намного меньше амплитуды, требуемой для
достижения потенциального барьера в точке G (![]() ), где скорость
замедляется и может возникнуть заметная фазовая задержка. Причиной столь малой амплитуды
установившихся колебаний, очевидно, является недостаточная амплитуда возбуждающей
силы. Однако дополнительная проверка показывает, что в условиях рис.5 увеличение
амплитуды возбуждения выше
), где скорость
замедляется и может возникнуть заметная фазовая задержка. Причиной столь малой амплитуды
установившихся колебаний, очевидно, является недостаточная амплитуда возбуждающей
силы. Однако дополнительная проверка показывает, что в условиях рис.5 увеличение
амплитуды возбуждения выше ![]() приводит к преодолению
потенциального барьера (точка G) с соответствующим уходом системы на бесконечность.
В то же время, как можно видеть из пунктирной кривой на рис.5б, на начальном участке
левее точки
приводит к преодолению
потенциального барьера (точка G) с соответствующим уходом системы на бесконечность.
В то же время, как можно видеть из пунктирной кривой на рис.5б, на начальном участке
левее точки ![]() как собственная возвращающая сила осциллятора,
так и приложенная к нему внешняя сила действуют в одном направлении. В результате
такого сложения сил осциллятор, несмотря на значительное затухание, в течение первой
четверти периода, начиная свой путь значительно выше уровня потенциального барьера
(точка P, соответствующая
как собственная возвращающая сила осциллятора,
так и приложенная к нему внешняя сила действуют в одном направлении. В результате
такого сложения сил осциллятор, несмотря на значительное затухание, в течение первой
четверти периода, начиная свой путь значительно выше уровня потенциального барьера
(точка P, соответствующая ![]() , где потенциал
, где потенциал ![]() составляет около
составляет около ![]() при
высоте барьера около
при
высоте барьера около ![]() ), доходит до точки Q, почти достигая
барьера при
), доходит до точки Q, почти достигая
барьера при ![]() (точка G). Таким образом, даже столь
небольшая внешняя сила, как едва превышающая
(точка G). Таким образом, даже столь
небольшая внешняя сила, как едва превышающая ![]() , уже приводит
к перевалу через потенциальный барьер и уходу системы на бесконечность.
, уже приводит
к перевалу через потенциальный барьер и уходу системы на бесконечность.
Причиной сложения действия внутренней и внешней сил является совпадение по фазе максимального начального отклонения с максимумом вынуждающей силы (косинуса). То есть, если такое фазовое соотношение нарушить, то нарушится и сложение сил, так что можно ожидать значительного повышения амплитуды возбуждения без ухода системы на бесконечность.
Проще всего положить начальное
отклонение равным нулю. Это и было сделано при построении разверток во времени,
приведенных на рис.4. Однако в наиболее интересном случае более или менее регулярной
двухамплитудной кривой, приведенном на рис.4г, при таком отклонении по времени от
нуля до ![]() , наблюдался начальный участок установления
колебаний, в пределах которого глубина модуляции возрастала от
, наблюдался начальный участок установления
колебаний, в пределах которого глубина модуляции возрастала от ![]() до
до ![]() . В ходе
дополнительной проверки было выявлено, что протяженность этого участка сильно зависит
от величины начального отклонения, таким образом, что с увеличением отклонения в
отрицательную сторону, то есть когда внутренняя и внешняя силы вычитаются, протяженность
участка установления уменьшается вплоть до нуля при
. В ходе
дополнительной проверки было выявлено, что протяженность этого участка сильно зависит
от величины начального отклонения, таким образом, что с увеличением отклонения в
отрицательную сторону, то есть когда внутренняя и внешняя силы вычитаются, протяженность
участка установления уменьшается вплоть до нуля при ![]() . При этом
вынужденные колебания сразу возбуждаются с глубиной модуляции в
. При этом
вынужденные колебания сразу возбуждаются с глубиной модуляции в ![]() и далее остаются регулярными, подобно показанным
на рис.4в, но с более глубокой модуляцией. В таких условиях амплитуда возбуждающей
силы без ухода системы на бесконечность может быть увеличена до
и далее остаются регулярными, подобно показанным
на рис.4в, но с более глубокой модуляцией. В таких условиях амплитуда возбуждающей
силы без ухода системы на бесконечность может быть увеличена до ![]() . Это и было сделано при построении кривых,
представленных на рис.6, к рассмотрению которых далее и перейдем.
. Это и было сделано при построении кривых,
представленных на рис.6, к рассмотрению которых далее и перейдем.
Рис.6. Колебания осциллятора с квадратичной нелинейностью
при специфическом выборе начального отклонения: ![]() .
.
а – вынуждающая сила;
б – смещение осциллятора во времени; справа – зависимость потенциала от координаты осциллятора, штриховкой показана окрестность потенциального барьера; горизонтальные пунктирные и точечные линии – значения координаты, соответствующие характерным уровням потенциала;
в – скорость движения осциллятора во времени.
Точки ![]() ,
, ![]()
![]() – характерные позиции вынуждающей
силы, смещения и скорости.
– характерные позиции вынуждающей
силы, смещения и скорости.
Параметры: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
На рис.6а показана развертка
во времени возбуждающей силы. Отличие от рис.5а состоит только в коэффициенте нормировки,
здесь равном ![]() . Точки
. Точки ![]() отмечают
наиболее характерный участок развития колебаний осциллятора, соответствующий одному
полному периоду. Далее во времени такие участи периодически повторяются, поэтому
отдельно не рассматриваются.
отмечают
наиболее характерный участок развития колебаний осциллятора, соответствующий одному
полному периоду. Далее во времени такие участи периодически повторяются, поэтому
отдельно не рассматриваются.
На рис.6б показано развитие
колебаний осциллятора во времени. На участке от ![]() до
до ![]() направления внутренней и внешней сил совпадают,
поэтому осциллятор проходит весь путь от одного крайнего положения до другого. Но
уже начиная с точки
направления внутренней и внешней сил совпадают,
поэтому осциллятор проходит весь путь от одного крайнего положения до другого. Но
уже начиная с точки ![]() внешняя сила стремится повернуть
назад готовый уйти на бесконечность осциллятор, в результате чего он возвращается
обратно в направлении к дну ямы. Однако из-за долгого пребывания в области потенциального
барьера (точка G), где скорость осциллятора крайне мала (как видно из рис.6в – скорость
между точками
внешняя сила стремится повернуть
назад готовый уйти на бесконечность осциллятор, в результате чего он возвращается
обратно в направлении к дну ямы. Однако из-за долгого пребывания в области потенциального
барьера (точка G), где скорость осциллятора крайне мала (как видно из рис.6в – скорость
между точками ![]() и
и ![]() проходит
через нуль), осциллятор в своем движении вверх к очередному моменту изменения полярности
вынуждающей силы (точка
проходит
через нуль), осциллятор в своем движении вверх к очередному моменту изменения полярности
вынуждающей силы (точка ![]() , где плюс меняется на минус),
не успевает дойти до верхнего края потенциальной ямы (точка D) и в точке
, где плюс меняется на минус),
не успевает дойти до верхнего края потенциальной ямы (точка D) и в точке ![]() даже слегка не доходит до ее дна (точка
E). Дальше осциллятор движется под действием взаимно противоположных сил: внутренней,
направленной вверх и внешней – вниз, поэтому, пройдя по инерции через небольшой
максимум, все же поворачивает вниз к точке
даже слегка не доходит до ее дна (точка
E). Дальше осциллятор движется под действием взаимно противоположных сил: внутренней,
направленной вверх и внешней – вниз, поэтому, пройдя по инерции через небольшой
максимум, все же поворачивает вниз к точке ![]() , где направление
внешней силы снова меняется и теперь уже совпадает с направлением внутренней. В
этой точке скорость осциллятора, еще раз пройдя через нуль (точка
, где направление
внешней силы снова меняется и теперь уже совпадает с направлением внутренней. В
этой точке скорость осциллятора, еще раз пройдя через нуль (точка ![]() на рис.6в), будучи направленной вверх, снова
возрастает и осциллятор достаточно быстро приходит в точку
на рис.6в), будучи направленной вверх, снова
возрастает и осциллятор достаточно быстро приходит в точку ![]() , соответствующую начальному уровню в точке
, соответствующую начальному уровню в точке
![]() . При этом внешняя сила также принимает то
же начальное значение (точка
. При этом внешняя сила также принимает то
же начальное значение (точка ![]() эквивалентна точке
эквивалентна точке ![]() ), в результате чего осциллятор по всем условиям
(положению, скорости и действующим силам) приходит в исходное положение и цикл колебаний
во времени повторяется.
), в результате чего осциллятор по всем условиям
(положению, скорости и действующим силам) приходит в исходное положение и цикл колебаний
во времени повторяется.
Можно видеть, что сформированная
таким образом зависимость положения осциллятора от времени (рис.6б, сплошная линия)
как раз повторяет отмеченный при рассмотрении рис.4г двухамплитудный с двойным периодом
характер полностью установившихся колебаний (при ![]() ).
).
Наличие наблюдаемого на рис.6б участка установления, как уже отмечалось, связано с выбором начального отклонения осциллятора равным нулю. При этом процесс установления состоит в постепенном выборе рассогласования фаз колебаний осциллятора с возбуждающей силой, за счет внутреннего затухания осциллятора постепенно сводящего такое рассогласование к стационарному значению, соответствующему регулярному характеру колебаний.
Таким образом, можно сделать вывод, что основной причиной формирования двухамплитудного с двойным периодом характера колебаний является фазовая задержка движения осциллятора при его нахождении в ближней окрестности потенциального барьера, где его движение резко замедляется.
12. Необходимые условия регулярного двухамплитудного режима
В разделе №3 приведена схематичная
классификация четырех основных режимов колебаний рассматриваемой системы. При этом
рассмотренные в разделах №10 и №11 колебания следует отнести к варианту режима №2
– регулярных колебаний с модуляцией амплитуды (автомодулированных). В этих разделах
в деталях был рассмотрен механизм формирования автомодуляции для случая двухамплитудного
режима, при котором исходный период возбуждающей силы удваивается. Однако из рассмотрения
рис.6б можно видеть, что при своем возвращении осциллятор после прохождения точки
![]() может еще несколько не дойти до уровня
может еще несколько не дойти до уровня ![]() (отмечен горизонтальным пунктиром), когда
полярность тянущей силы (рис.6а) после прохождения точки
(отмечен горизонтальным пунктиром), когда
полярность тянущей силы (рис.6а) после прохождения точки ![]() уже изменится и будет стремиться заставить
осциллятор двигаться вниз (в направлении дна ямы). В результате точка
уже изменится и будет стремиться заставить
осциллятор двигаться вниз (в направлении дна ямы). В результате точка ![]() придется ниже уровня
придется ниже уровня ![]() , так что цикл изменения амплитуды за два периода
возбуждающей силы может не закончиться, то есть на его завершение осциллятору потребуется
позаимствовать еще какую-то дополнительную часть следующего периода возбуждения.
Такая задержка во времени может привести к тому, что результирующий период колебаний
осциллятора будет превышать период возбуждения не в два, а в какое-то большее, в
том числе дробное число раз. То есть колебания осциллятора примут как раз такой
вид, как был отмечен при описании режима №2, причем главным классификационным признаком
здесь будет являться периодичность.
, так что цикл изменения амплитуды за два периода
возбуждающей силы может не закончиться, то есть на его завершение осциллятору потребуется
позаимствовать еще какую-то дополнительную часть следующего периода возбуждения.
Такая задержка во времени может привести к тому, что результирующий период колебаний
осциллятора будет превышать период возбуждения не в два, а в какое-то большее, в
том числе дробное число раз. То есть колебания осциллятора примут как раз такой
вид, как был отмечен при описании режима №2, причем главным классификационным признаком
здесь будет являться периодичность.
Необходимым условием такого режима является наличие на одном из краев потенциальной ямы барьера с достаточно пологим подходом к точке максимума. Степень пологости подхода должна быть такова, чтобы скорость осциллятора на этом участке уменьшалась настолько, что время поворота движения осциллятора в обратном направлении значительно превышало время периода возбуждающей силы. При этом в движении осциллятора образуется фазовая задержка относительно колебаний возбуждающей силы, в результате чего осциллятор за один период возбуждения вернуться к исходному положению не успевает.
Можно полагать, что необходимым условием периодичности является требование полного повторения движения осциллятора в области поворота на пологом участке потенциала. Однако возможны условия, при которых такая повторяемость может нарушаться, рассмотрению которых посвящен следующий раздел.
13. Модель стохастизации автоколебаний
В предыдущем разделе отмечено, что необходимым условием периодичности колебаний осциллятора, свойственной режиму №2 (раздел №3), является полная повторяемость движения осциллятора в области поворота в тех случаях, когда он в эту область попадает. Однако в точке вершины барьера (G на рис.5б и 6б) потенциал имеет горизонтальную касательную, поэтому скорость вблизи этой точки может падать почти до нуля и осциллятор может находиться в ней неопределенно долго. Для более подробного пояснения такой ситуации рассмотрим рис.7, где показана схема формирования времени задержки осциллятора вблизи потенциального барьера (масштаб произвольный, выбран, исходя из большей наглядности рисунка). На рисунке рассмотрено действие только потенциальной силы. Вынуждающая сила складывается с потенциальной примерно так, как это показано на рис.5б и 6б, поэтому здесь не рассматривается.
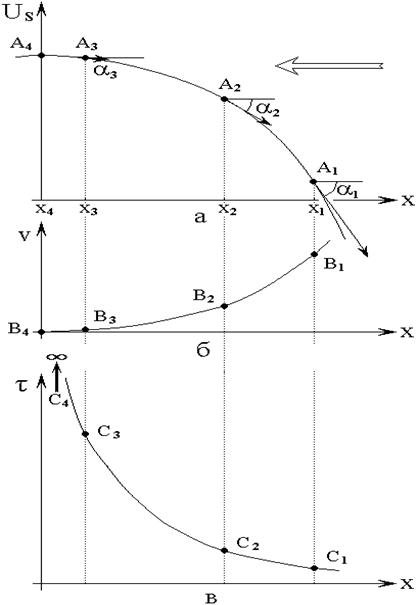
Рис.7. Схема формирования
неопределенно длительной задержки осциллятора вблизи потенциального барьера (масштаб
условный).
а – потенциал; б – скорость; в – время задержки.
На рис.7а показан барьер потенциала.
По горизонтальной оси отложена координата ![]() . Открытой
стрелкой справа показано направление движения осциллятора, последовательно проходящего
точки
. Открытой
стрелкой справа показано направление движения осциллятора, последовательно проходящего
точки ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где потенциал
принимает значения
, где потенциал
принимает значения ![]() ,
, ![]() ,
, ![]() ,
, ![]() . В каждой
из этих точек стрелкой, касательной к кривой
. В каждой
из этих точек стрелкой, касательной к кривой ![]() , показано
направление потенциальной силы, как производной от потенциала по координате. Длина
стрелки отражает абсолютную величину силы.
, показано
направление потенциальной силы, как производной от потенциала по координате. Длина
стрелки отражает абсолютную величину силы.
Полагая, что на осциллятор действует компонента силы, параллельная горизонтальной оси, то есть:
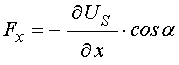 , (57)
, (57)
можно видеть, что по мере приближения
осциллятора к барьеру, несмотря на уменьшение угла ![]() , сила,
скатывающая осциллятор в яму, уменьшается, а в точке
, сила,
скатывающая осциллятор в яму, уменьшается, а в точке ![]() (вершина
барьера) вообще становится равной нулю.
(вершина
барьера) вообще становится равной нулю.
На рис.7б показана скорость,
которую приобретает осциллятор под действием приложенной к нему силы. Можно видеть,
что скорость тем больше, чем точка расположения осциллятора дальше отстоит от вершины
потенциального барьера. Так скорость максимальна в точке ![]() , где равна
, где равна![]() , а в точке
, а в точке
![]() скорость равна
скорость равна![]() , то есть
стремится к нулю.
, то есть
стремится к нулю.
На рис.7в показано время задержки
осциллятора вблизи вершины барьера, определяемое как величина, обратная скорости.
При этом, когда скорость в точке ![]() стремится к нулю, то время
задержки
стремится к нулю, то время
задержки ![]() в той же точке стремится к бесконечности.
Поскольку зависимость времени задержки от координаты является гиперболой, то вблизи
вершины барьера исчезающе малые изменения координаты могут вызвать большие изменения
времени задержки, то есть в значительных пределах менять фазу движения осциллятора
относительно вынуждающей силы. Такое сильное изменение параметрически определенной
функции под действием малого изменения параметра может быть причиной стохастической
неустойчивости колебаний [31]. При этом следующие друг за другом малые изменения
параметра, в результате накопления больших изменений состояния системы, приводят
к тому, что с течением времени система «забывает» начальное состояние и движение
в целом приобретает стохастический характер.
в той же точке стремится к бесконечности.
Поскольку зависимость времени задержки от координаты является гиперболой, то вблизи
вершины барьера исчезающе малые изменения координаты могут вызвать большие изменения
времени задержки, то есть в значительных пределах менять фазу движения осциллятора
относительно вынуждающей силы. Такое сильное изменение параметрически определенной
функции под действием малого изменения параметра может быть причиной стохастической
неустойчивости колебаний [31]. При этом следующие друг за другом малые изменения
параметра, в результате накопления больших изменений состояния системы, приводят
к тому, что с течением времени система «забывает» начальное состояние и движение
в целом приобретает стохастический характер.
В рассматриваемой задаче это приводит к квазихаотическим колебаниям, классифицированным в разделе №3 как режим №3.
Таким образом, необходимым условием квазихаотического характера колебаний является приближение осциллятора к вершине потенциального барьера настолько близко, что малые изменения его координаты приводят к большому изменению времени задержки, то есть решающую роль играет задержка во времени пребывания осциллятора в окрестности вершины потенциального барьера, а также соотношение между временем такой задержки и периодом возбуждающей силы.
14. Модель динамического фазового перехода
Рассмотрим условия формирования стохастического режима колебаний более подробно. Потенциальный барьер потенциала третьего порядка (52) (рис.3а) можно рассматривать как границу между двумя принципиально различными динамическими состояниями системы. Правее этой границы имеют место ограниченные колебания, левее – уход системы на бесконечность.
Переход системы через вершину потенциального барьера можно рассматривать как переход из одного состояния в другое – из ограниченного колебательного в безгранично нарастающее. Для описания такого перехода воспользуемся аппаратом, подобным развитому Л.Д.Ландау для фазовых переходов второго рода [37]. В качестве «параметра порядка» возьмем отклонение координаты осциллятора от точки, соответствующей вершине потенциального барьера.
Рассмотрим рис.8, иллюстрирующий развитие во времени координаты осциллятора и его скорости по мере приближения к барьеру.
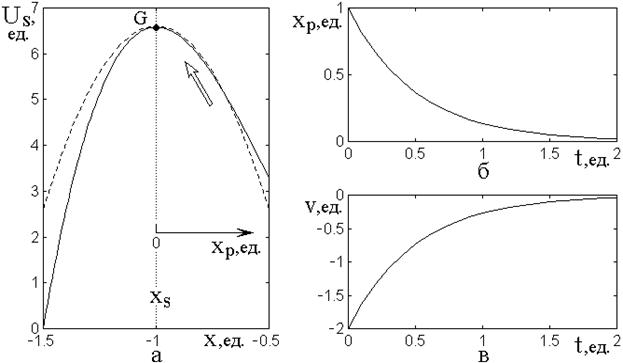
Рис.8. Потенциальный барьер (а) и развитие во времени относительной координаты осциллятора (параметра порядка) (б) и его скорости (в) по мере приближения к вершине барьера.
На рис.8а сплошной линией показан потенциальный барьер, соответствующий кубическому потенциалу вида (52):
 , (58)
, (58)
построенному при параметрах ![]() ,
, ![]() . Вершина
барьера, соответствующая координате
. Вершина
барьера, соответствующая координате ![]() обозначена буквой G. Параметр
порядка имеет вид:
обозначена буквой G. Параметр
порядка имеет вид:
![]() , (59)
, (59)
то есть в точке ![]() равен нулю. Разложение потенциала с точностью
до второй степени параметра порядка имеет вид:
равен нулю. Разложение потенциала с точностью
до второй степени параметра порядка имеет вид:
![]() , (60)
, (60)
где ![]() – постоянное
слагаемое, которое определяется совпадением исходного потенциала и его разложения
в точке
– постоянное
слагаемое, которое определяется совпадением исходного потенциала и его разложения
в точке ![]() .
.
При принятых при построении
рис.3а параметрах оптимальное разложение получается при ![]() и
и
![]() , то есть получаем:
, то есть получаем:
![]() . (61)
. (61)
Построенный по этой формуле
потенциал показан на рис.8а пунктирной линией. Видно, что до уровня ![]() расхождение сплошной и пунктирной кривой не
превышает
расхождение сплошной и пунктирной кривой не
превышает ![]() . Стрелкой вверху показано направление движения
осциллятора по мере того, как он взбирается на барьер.
. Стрелкой вверху показано направление движения
осциллятора по мере того, как он взбирается на барьер.
В теории релаксации параметра порядка фазового перехода второго рода Ландау-Халатникова [37, стр.517] предполагается, что скорость изменения этого параметра пропорциональна производной от потенциала по координате.
Для оценки характера изменения скорости осциллятора от времени по мере приближения к барьеру, воспользуемся аналогичным предположением, то есть будем считать, что эта скорость пропорциональна действующей на осциллятор потенциальной силе:
где ![]() – постоянный
коэффициент.
– постоянный
коэффициент.
Для оценки величины этого
коэффициента решим уравнение (62) относительно ![]() (например,
методом разделения переменных [38]). При этом с точностью до постоянного коэффициента
получаем:
(например,
методом разделения переменных [38]). При этом с точностью до постоянного коэффициента
получаем:
то есть параметр порядка релаксирует во времени с постоянной
![]() . (64)
. (64)
Из этого выражения находим искомый коэффициент пропорциональности в выражении (62):
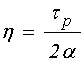 . (65)
. (65)
Согласно выполненному в разделах
№10 и №11 рассмотрению фазовой задержки, можно полагать, что для успешной реализации
квазихаотического режима время релаксации параметра порядка ![]() должно превышать длительность периода возбуждения
должно превышать длительность периода возбуждения
![]() , то есть должно выполняться неравенство
, то есть должно выполняться неравенство ![]() . Для численной оценки положим, что такое превышение
выполняется вдвое, то есть:
. Для численной оценки положим, что такое превышение
выполняется вдвое, то есть: ![]() , откуда получаем:
, откуда получаем:
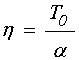 . (66)
. (66)
При принятых при построении
рис.3 параметрах с учетом ![]() , получаем:
, получаем: ![]() .
.
Выражение (63) принимает вид:
![]() . (67)
. (67)
Зависимость параметра порядка
от времени, построенная по этой формуле, имеет вид, показанный на рис.8б. Видно,
что уже за время действия первого периода вынуждающей силы (при ![]() ) параметр порядка уменьшается до величины
) параметр порядка уменьшается до величины
![]() от своего начального значения, а при времени
двух периодов (
от своего начального значения, а при времени
двух периодов (![]() ) падает почти до нуля (до
) падает почти до нуля (до ![]() ).
).
Для оценки скорости изменения
параметра порядка ![]() воспользуемся соотношением
(62), где
воспользуемся соотношением
(62), где ![]() найдем из (52). В результате получаем:
найдем из (52). В результате получаем:
![]() . (68)
. (68)
Подставляя ![]() в
соответствии с (63), находим:
в
соответствии с (63), находим:
![]() . (69)
. (69)
Построенная по этой формуле
зависимость скорости от времени показана на рис.8в. Можно видеть, что за время двух
периодов возбуждения (![]() ) скорость падает почти до нуля,
а дальше уменьшается еще более по экспоненциальному закону.
) скорость падает почти до нуля,
а дальше уменьшается еще более по экспоненциальному закону.
Соответствующее время фазовой задержки с точностью до постоянного коэффициента принимает вид:
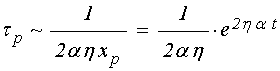 , (70)
, (70)
то есть во времени возрастает по экспоненте, что и обеспечивает необходимое для реализации стохастического режима сильное изменение фазы при малом изменении координаты осциллятора.
Следует отметить, что столь сильное изменение фазы возможно только в ближайшей окрестности потенциального барьера, тогда как при некотором удалении от него изменение фазы уже не будет столь значительным и вместо квазихаотического режима №3 реализуется более или менее регулярный режим №2. То есть резкой границы между этими режимами нет и переход является плавным и беспороговым. Можно полагать, что переход от регулярного режима к нерегулярному сопровождается заметным расширением спектра колебаний, что могло бы служить критерием такого перехода. Заметим, что поиск подобного критерия мог бы явиться предметом самостоятельного исследования.
Замечание. Следует заметить, что рассмотренный здесь переход системы от колебаний внутри ямы к уходу на бесконечность в классическом смысле фазовым переходом не является, так как здесь нет двух различных состояний вещества как двух различных фаз. Однако по обе стороны от барьера здесь имеют место два различных динамических состояния осциллятора, переход между которыми по амплитуде возбуждения носит пороговый характер. Примененный здесь математический аппарат близок к традиционному аппарату описания фазовых переходов [37], поэтому предложенная здесь модель по аналогии названа «моделью динамического фазового перехода».
15. Критичность стохастического режима
В предыдущем разделе на примере
кубического потенциала для одного осциллятора показано, что условия, требуемые для
возбуждения квазихаотического режима №4, выполняются. Однако более подробная проверка
показывает, что в случае единственного осциллятора интервал параметров режима №4
является крайне узким. Так из рис.4д и 4е можно видеть, что колебания, приближаясь
к хаотичности, все же сохраняют значительный элемент регулярности. Действительно,
при увеличении амплитуды возбуждения от ![]() (рис.4д)
до
(рис.4д)
до ![]() (рис.4е), то есть всего на
(рис.4е), то есть всего на ![]() , довольно регулярный режим (хотя и осложненный
вторичной модуляцией) уже сменяется уходом системы на бесконечность. Поэтому успешная
реализация квазихаотического режима для одного осциллятора в известной степени затруднена
(что, по крайней мере, относится к исследованному здесь случаю совпадения частот).
Однако для системы из двух осцилляторов квазихаотический режим реализуется уже в
полной мере. Особенно хорошо это наблюдается на
рис.2в в работе [30], где нерегулярность
проявляется для обоих осцилляторов в равной степени, причем колебания одного из
них от колебаний другого заметно отличаются. Можно полагать, что для рассмотрения
механизма таких колебаний, наряду с бесфлуктуационной моделью фазового перехода,
надо учитывать флуктуации параметра порядка. Более того, учет флуктуаций, вследствие
их случайного характера, может позволить описать условия ухода системы на бесконечность,
происходящего не сразу после включения возбуждения, а по прошествии нескольких переколебаний,
подобно тому, как это показано на рис.4е. Однако этот вопрос также требует более
подробного исследования.
, довольно регулярный режим (хотя и осложненный
вторичной модуляцией) уже сменяется уходом системы на бесконечность. Поэтому успешная
реализация квазихаотического режима для одного осциллятора в известной степени затруднена
(что, по крайней мере, относится к исследованному здесь случаю совпадения частот).
Однако для системы из двух осцилляторов квазихаотический режим реализуется уже в
полной мере. Особенно хорошо это наблюдается на
рис.2в в работе [30], где нерегулярность
проявляется для обоих осцилляторов в равной степени, причем колебания одного из
них от колебаний другого заметно отличаются. Можно полагать, что для рассмотрения
механизма таких колебаний, наряду с бесфлуктуационной моделью фазового перехода,
надо учитывать флуктуации параметра порядка. Более того, учет флуктуаций, вследствие
их случайного характера, может позволить описать условия ухода системы на бесконечность,
происходящего не сразу после включения возбуждения, а по прошествии нескольких переколебаний,
подобно тому, как это показано на рис.4е. Однако этот вопрос также требует более
подробного исследования.
Заключение
Рассмотрены нелинейные вынужденные колебания намагниченности и упругого смещения в нормально намагниченной ферритовой пластине, обладающей магнитоупругими свойствами. Исходная задача, содержащая семь уравнений первого порядка и четыре граничных условия, сведена к квадрированной системе из двух уравнений второго порядка без граничных условий. Путем численного решения квадрированной системы выявлены четыре принципиально различных режима колебаний: режим №1 – колебания регулярные без модуляции (синусоидальные); режим №2 – колебания с ограниченной амплитудой и регулярной модуляцией (автомодулированные); режим №3 – колебания с ограниченной амплитудой и квазислучайной модуляцией (квазистохастические); режим №4 – колебания с неограниченно нарастающей амплитудой (уход системы на бесконечность).
С целью максимальной формализации рассматриваемой задачи получена обобщенная система уравнений, описывающая вынужденные колебания двух связанных осцилляторов. Показано, что присутствующая в такой системе уравнений связь осцилляторов не только через переменные, но и через производные, обусловлена спецификой исходной магнитоупругой системы, для полного описания которой, вследствие ее гиромагнитной природы, требуется пять уравнений первого порядка, что эквивалентно колебаниям системы с двумя с половиной степенями свободы.
В процессе исследования ухода системы на бесконечность (режим №4) показано, что в его основе могут лежать два принципиально различных механизма: при наличии связи через производные – связь через переменные, линейная в обоих уравнениях; в отсутствие связи через производные – связь через переменные, квадратичная в первом уравнении и линейная во втором. Первый из этих механизмов может быть интерпретирован на основе модели отрицательного сопротивления, второй – на основе модели потенциала. С помощью представления потенциала в виде степенной функции обеих переменных показано, что для ухода системы на бесконечность необходимым условием является нечетность какого-либо из степенных слагаемых, тогда как четность может компенсировать уход на бесконечность, обусловленную слагаемыми со степенью на единицу меньшей.
Записана упрощенная система, содержащая связь только через переменные не выше третьего порядка, соответствующую потенциалу четвертого порядка. Показано, что, благодаря наличию двух с половиной степеней свободы, потенциалы для каждого из уравнений должны отличаться друг от друга, давая собственный вклад в обобщенные силы.
Рассмотрена возможность возбуждения в такой системе колебаний автомодуляционного характера. Показано, что наиболее простым достаточным условием существования таких колебаний, при действии возбуждения только на первый осциллятор, является наличие в первом уравнении слагаемого второго порядка, а во втором – первого. Показано, что в силу подобия колебаний второго осциллятора колебаниям первого, достаточно рассмотреть вынужденные колебания только одного осциллятора с квадратичной нелинейностью, потенциал для которого является кубическим.
Рассмотрены свободные и вынужденные колебания осциллятора с кубическим потенциалом. Показано, что свободные колебания возможны только в пределах потенциальной ямы, ограниченной с одной стороны бесконечным ростом потенциала, а с другой – потенциальным барьером, по обратную сторону от которого потенциал стремится к минус бесконечности. Для вынужденных колебаний возможны все четыре основных режима, сменяющие друг друга по мере увеличения амплитуды возбуждения, причем первые три режима реализуются внутри потенциальной ямы, а четвертый – с выходом из нее за пределы потенциального барьера.
На основе последовательного рассмотрения различных этапов развития колебаний во времени построена модель фазовой задержки, позволяющая объяснить значительное (на несколько периодов) рассогласование фаз колебаний осциллятора относительно вынуждающей силы. Путем аналогичного рассмотрения построена модель двухамплитудных колебаний, являющихся частным случаем режима №2 – регулярных автоколебаний с модулированной амплитудой. Показано, что решающую роль здесь играет задержка вынужденных колебаний относительно действующей силы, обусловленная уменьшением скорости движения в ближней окрестности точки максимума барьера потенциала. При этом периодичность колебаний проявляется в повторении от цикла к циклу одного и того же движения осциллятора в области поворота на пологом близком к вершине барьера участке потенциала.
Рассмотрены условия возможности реализации квазихаотического характера колебаний осциллятора (режим №3). Показано, что необходимым условием такого режима является приближение осциллятора к вершине потенциального барьера настолько близко, что малые изменения его координаты приводят к большому изменению времени задержки. Для интерпретации увеличения времени задержки предложена модель динамического фазового перехода, предполагающая скорость изменения отклонения координаты осциллятора от максимума барьера (параметра порядка) пропорциональной величине действующей на осциллятор потенциальной силе. На основе предложенной модели оценена степень зависимости времени задержки осциллятора вблизи вершины барьера от величины приближения к ней. Показано, что по мере приближения осциллятора к барьеру время задержки возрастает экспоненциальным образом, стремясь к бесконечности, что и является причиной стохастизации колебаний.
На основе сравнения квазихаотических режимов для одного и двух осцилляторов показано, что в случае двух осцилляторов стохастичность колебаний выражена значительно сильнее, чем для одного, причем подобие колебаний второго осциллятора колебаниям первого в значительной степени нарушается.
Благодарность
Авторы признательны к.ф.-м.н. В.С.Власову (СыктГУ) за первичную постановку задачи, помощь на предварительных этапах и постоянное стимулирующее внимание к работе.
Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).
Литература
1. Физическая энциклопедия. Т.1. М.: Советская энциклопедия. 1988. Статья «Гиперзвук».
2. Такер Дж., Рэмптон В., Гиперзвук в физике твердого тела. М.: Мир. 1975.
3. Поверхностные акустические волны. Под ред. Олинера А. М.: Мир. 1981.
4. Викторов И.А. Звуковые поверхностные волны в твердых телах. М.: Наука. 1981.
5. Bleustein J.L. // Appl. Phys. Lett. 1968. V.13. P.412.
6. Гуляев Ю.В. // ПЖЭТФ. 1969. Т.9. С.63.
7. Кикучи Е. Ультразвуковые преобразователи. М.: Мир. 1972.
8. Голямина И.П. // Магнитострикционные излучатели из ферритов. В кн.: Физика и техника мощного ультразвука. Кн.1. Источники мощного ультразвука. М.: Наука. 1967.
9. Физическая акустика. Под ред. Мэзона У., Терстона Р. Т.1-7. М.: Мир. 1966-1974.
10. Comstock R.L., LeCraw R.C. // J. Appl. Phys. 1963. V.34. № 10. P.3022.
11. Suhl H. // J. Phys. Chem. Sol. 1957. V.1. №4. P.209.
12. Моносов Я.А. // Нелинейный ферромагнитный резонанс. М.: Наука. 1971.
13. Захаров В.Е., Львов В.С., Старобинец С.С. // УФН. 1974. Т.114. №4. С.609.
14. Temiryazev A.G., Tikhomirova M.P., Zilberman P.E. // J. Appl. Phys. 1994. V.76. №12. P.5586.
15. Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ЖЭТФ. 1995. Т.108. №1. С.281.
16. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // РЭ. 1999. Т.44. № 10. С.1262.
17. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ФТТ. 2000 Т.42. №6. С.1062.
18. Gerrits Th., Schneider M.L., Kos A.B., Silva T.J. // Phys.Rev.B. 2006. V.73. №9. P.094454(7).
19. Власов В.С. Исследование релаксационной и нелинейной динамики магнитных и магнитоупругих колебаний пленок и частиц. Диссертация на соискание ученой степени канд. физ.-мат. наук. МГУ. 2007.
20. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.
21. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники", 2013, №11, c.1-38.
http://jre.cplire.ru/jre/nov13/3/text.html, http://jre.cplire.ru/jre/nov13/3/text.pdf.
22. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники", 2014, №1, c.1- 42.
http://jre.cplire.ru/jre/jan 14/11/text.html, http://jre.cplire.ru/jre/jan 14/11/text.pdf.
23. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // РЭ. 2015. Т.60. №1. С.79.
24. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // РЭ. 2015. Т.60. №3. С.297.
25. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // Сборник трудов XXI Международной конференции «Электромагнитное поле и материалы». М.: НИУ МЭИ. 2013. С.188.
26. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // Сборник трудов XXI Международной конференции «Электромагнитное поле и материалы». М.: НИУ МЭИ. 2013. С.199.
27. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // Сборник материалов X Международной зимней школы-семинара «Хаотические автоколебания и образование структур» (ХАОС-2013). Саратов: Изд. центр «Наука». 2013. С.78.
28. Котов Л.Н., Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // Вестник Челябинского государственного университета. 2013. №25 (316). Физика. Вып.18. С.27.
29. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». М.: НИУ МЭИ. 2014. С.161.
30. Иванов А.П., Шавров В.Г., Щеглов В.И. // Электронный «Журнал радиоэлектроники». 2015. №5. http://jre.cplire.ru/jre/may15/4/text.html,
http://jre.cplire.ru/jre/may15/4/text.pdf.
31. Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику. М.: Наука. 1988.
32. Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. М.: Физматлит. 2003.
33. Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М.: Наука. 1978.
34. Лагранж Ж. Аналитическая механика, т.1,2. М.: Гостехиздат. 1950.
35. Ландау Л.Д., Лифшиц Е.М. Механика (Теоретическая физика, т.I). М.: Наука. 1965.
36. Ольховский И.И. Курс теоретической механики для физиков. М.: Наука. 1970.
37. Лифшиц Е.М., Питаевский Л.П. Физическая кинетика (Теоретическая физика, т.Х). М.: Наука. 1979.
38. Степанов В.В. Курс дифференциальных уравнений. М.Л.: ОГИЗ. Гос. изд. техн.-теор. лит. 1945.