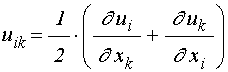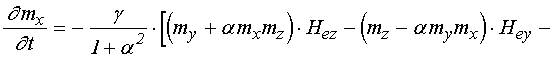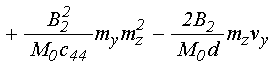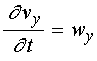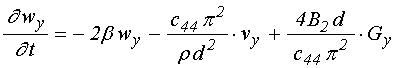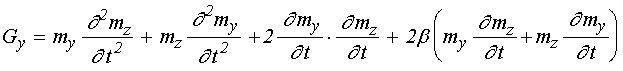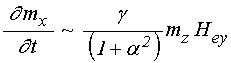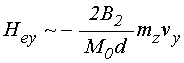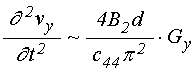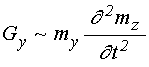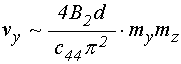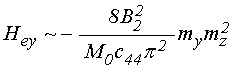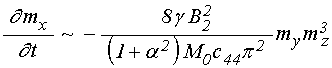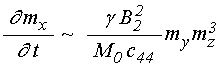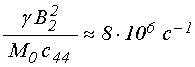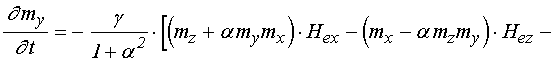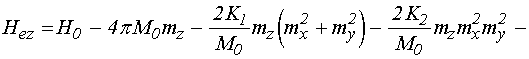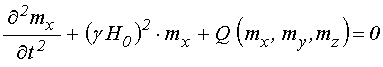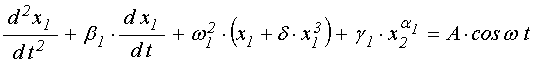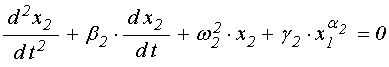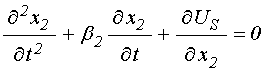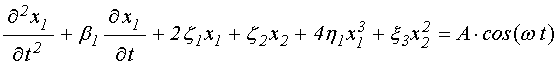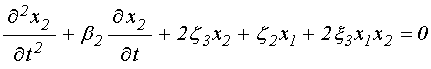"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2015

оглавление

УДК 537.874; 537.624

АНАЛИЗ АВТОМОДУЛЯЦИОННЫХ КОЛЕБАНИЙ В МАГНИТОУПРУГОЙ СРЕДЕ НА ОСНОВЕ МОДЕЛИ СВЯЗАННЫХ МАГНИТНОГО И УПРУГОГО ОСЦИЛЛЯТОРОВ

 

А. П. Иванов 1, В. Г. Шавров 2, В. И. Щеглов 2

 

1 Сыктывкарский государственный университет

2 Институт радиотехники и электроники им. В.А.Котельникова РАН

Статья получена 17 мая 2015 г.

 

Аннотация. Рассмотрены нелинейные вынужденные колебания намагниченности и упругого смещения в нормально намагниченной ферритовой пластине, обладающей магнитоупругими свойствами. Для моделирования таких колебаний предложена упрощенная система из двух связанных осцилляторов, один из которых обладает гиромагнитными свойствами. На основе такой модели показана возможность возбуждения вынужденных колебаний автомодуляционного характера. Выявлены шесть основных режимов автомодуляционных  колебаний, для интерпретации которых предложены две модели – обобщенного потенциала и генерации гармоник.

Ключевые слова: магнитоупругое взаимодействие, нелинейные колебания, автомодуляционный режим.

Abstract. The nonlinear forced vibrations of magnetization and elastic displacement in normal magnetized ferrite plate having magnetoelastic properties are investigated. For modeling of these vibrations the simplified system of two connected oscillators, one of which has magnetoelastic properties, is proposed. On the basis of this model the possibility of excitation of forced vibrations having auto-modulation character is shown. It is found six frame auto-modulation vibration regimes. For their interpretation two models are proposed: generalized potential and harmonic frequency generation.  

Key words: magnetoelastic interaction, nonlinear vibrations, auto-modulation regime. 

 

Введение

Возбуждение гиперзвуковых колебаний в диапазоне СВЧ актуально для общей физики [1], технической акустики [2], аналоговой обработки информации [3-6]. Весьма перспективными здесь являются ферритовые магнитострикционные преобразователи, работающие в условиях ферромагнитного резонанса (ФМР) [7]. Традиционными материалами для таких преобразователей являются железоиттриевый и тербиевый ферриты-гранаты (ЖИГ и ТбФГ), имеющие рекордно низкие потери и высокое значение константы магнитоупругого взаимодействия [7]. 

Помехой на пути повышения мощности таких преобразователей является рост потерь за счет параметрического возбуждения обменных спиновых волн [8], которого можно избежать только путем выбора геометрии преобразователя в виде нормально намагниченной тонкой пластины [9-13].

В работе [14] показано, что при этом амплитуда гиперзвука может превышать таковую в линейном режиме более чем в 30 раз. В двухслойной структуре [15,16] превышение достигает 70 раз, что открывает путь для создания высокомощных магнитоакустических преобразователей.

В работах [17-20] показано, что в таких структурах возможны колебания автомодуляционного характера. Такие колебания могут представлять значительный прикладной интерес в плане создания устройств как синхронного, так и несинхронного преобразования частоты гиперзвуковых колебаний, в том числе деления с кратностью отношения, достигающего нескольких порядков.

Расчет подобных  автомодуляционных колебаний в условиях ФМР требует привлечения весьма сложного математического аппарата, успешно реализуемого только ценой ряда упрощающих предположений. В простейшем варианте задача сводится к системе семи нелинейных дифференциальных уравнений первого порядка, разрешимой только численными методами [14]. Условия практики однако требуют создания достаточно простого расчетного аппарата, позволяющего оценить возможности и рассчитать основные параметры преобразователя без привлечения сложных аналитических и численных методов.

В работах [19,20] впервые показана возможность сведения полной задачи к модельной системе из двух связанных осцилляторов, один из которых обладает гиромагнитными свойствами. На основе упрощенной модели показана возможность возбуждения двух видов автомодуляционных колебаний – синхронного и асинхронного. Для асинхронных колебаний выявлены различные режимы: навязанный, стохастический, регулярный. Отмечена аналогия регулярного режима с наблюдаемыми в эксперименте автоколебаниями в системе «ферритовый диск – электромагнитный резонатор» [21-23]. 

В работах [24-27] предложен аппарат, позволяющий свести задачу о возбуждении гиперзвука магнитострикционным преобразователем в условиях ФМР к упрощенной модели возбуждения двух связанных осцилляторов – магнитного и упругого. При этом полная система, содержащая семь уравнений первого порядка и четыре граничных условия, в рамках квадратичного приближения сведена к квадрированной системе из четырех уравнений первого порядка без граничных условий. В работе [27] полученная система уравнений применена к анализу некоторых частных видов колебаний автомодуляционного характера. В работе [28] выявлены условия и приведены рекомендации выбора параметров материала преобразователя, требуемых для эффективной реализации автомодуляционного режима.

Однако рассмотрение, проведенное в перечисленных работах, является неполным. Так отсутствует достаточная классификация весьма разнообразной совокупности автомодуляционных режимов, недостаточно выявлены их пороговые свойства, не рассмотрены предельные возможности возбуждения в достаточно широком диапазоне изменения параметров материала.

Настоящая работа является обобщением и дальнейшим развитием перечисленных работ с целью выявления максимального разнообразия свойств автомодуляционных явлений. 

 

1. Геометрия гиромагнитного резонатора   

Поскольку основным предметом исследования являются вынужденные автомодуляционные колебания в гиромагнитном резонаторе, рассмотрим сначала общую постановку задачи для такого резонатора.  

    Подобно [14], будем рассматривать ферритовую пластину, намагниченную по нормали к ее плоскости, в геометрии, показанной на рис.1.

 

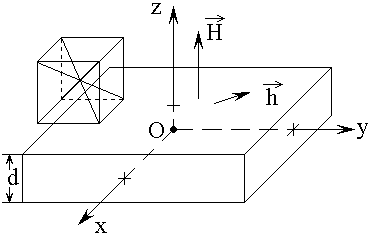
Рис.1. Геометрия задачи.

 

Полагаем, что феррит по магнитным свойствам –  изотропен, однако по упругим и магнитоупругим – обладает кубической симметрией, причем ось (100) перпендикулярна плоскости пластины. Будем считать, что упругие свойства описываются только константой  , а магнитоупругие – константой . Задача решается в декартовой системе координат , ось  которой перпендикулярна плоскости пластины. Внешнее поле имеет вид: , где  – постоянное подмагничивающее поле,  – компоненты переменного поля.

Полагая полную плотность энергии пластины  равной сумме плотностей магнитной, упругой и магнитоупругой энергий, подобно [14], получаем: 

          

                         ,              (1)

где  – нормированный вектор намагниченности,  – намагниченность насыщения; – координаты, ,  – тензор деформаций:

,                                                                  (2)

 

 – компоненты упругого смещения.

В выражении (1) присутствуют два вида переменных – намагниченность и упругое смещение. Будем полагать, что динамическое поведение намагниченности подчиняется уравнению Ландау-Лифшица [29,30], а динамическое поведение упругого смещения – уравнению толщинных упругих колебаний тонкой пластины [31]. Входящие в эти уравнения эффективные поля и упругие силы получаются из (1) стандартной процедурой дифференцирования по компонентам намагниченности и упругого смещения [29-31].  

Таким образом, в подобной постановке задачи присутствуют два связанных резонатора: магнитный и упругий, взаимодействие между которыми и рассматривается далее. 

 

2. Характер нелинейной связи для гиромагнитного резонатора

Следуя работе [19], рассмотрим сначала, каким образом реализуется нелинейная связь между магнитным и упругим резонаторами.

Согласно [14], достаточные для настоящего рассмотрения уравнения движения для случая однородной прецессии и первой упругой моды, имеют вид: (формулы (66), (74), (70), (72), (77) в работе [14]):

                                            ;                              (3)

 

                            ;                             (4)

;                                                                                            (5)

.                                 (6)

         (7)

 

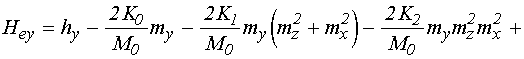
Оценим характер нелинейной связи между компонентами намагниченности, реализуемой за счет магнитоупругого взаимодействия в уравнении для .

Из (3) получаем:

.                                                                           (8)

 

Из (4) получаем:

.                                                                                    (9)

 

Из (5) и (6) получаем:

.                                                                       (10)

 

Из (7) получаем:

.                                                                                 (11)

 

Полагая зависимость от времени вида , выполняя дифференцирование в (10), (11) и сокращая на , получаем:

.                                                                          (12)

 

Подставляя (12) в (9), получаем:

.                                                                 (13)

 

Подставляя (13) в (8), получаем:

.                                             (14)

 

Полагая  и , а также отбрасывая несущественный для рассмотрения знак минус, получаем:

.                                                                    (15)

 

Таким образом, видим, что связь первого уравнения для намагниченности с другими осуществляется за счет члена четвертой степени по намагниченности.

Оценим коэффициент связи, при параметрах материала, типичных для железоиттриевого граната (ЖИГ) [7]: ; ;  , а также .

При этом получаем:

.                                                                         (16)

 

При однородном ферромагнитном резонансе в поле , соответствующем частоте , производная  составляет около , что более чем на порядок превышает величину полученного коэффициента связи (16), то есть в этом случае связь является довольно слабой. Однако при поле , соответствующем частоте , производная  составляет около , что по порядку равняется коэффициенту связи (16), то есть в этом случае роль связи может быть значительной.

Таким образом, можно видеть, что в магнитоупругой среде связь между компонентами намагниченности, имея четвертый порядок по намагниченности, прямо пропорциональна квадрату константы магнитоупругого взаимодействия, обратно пропорциональна намагниченности и константе упругости, причем проявляется тем сильнее, чем ниже частота возбуждения. 

Связь может быть весьма сильной в материалах с большой магнитострикцией и малой намагниченностью. Так, для тербиевого феррита-граната, где константа  более чем на порядок больше, а намагниченность на порядок меньше, чем в ЖИГ, при параметрах  ,   [7] и том же, что для ЖИГ значении константы упругости , получаем коэффициент связи равным , что обеспечивает сильную связь вплоть до частот порядка десятков гигагерц.

Полученный здесь коэффициент связи относится к уравнению (3), содержащему первую производную от намагниченности . Для получения уравнения второго порядка, каковым является классическое уравнение колебаний, продифференцируем (3) по времени еще раз и получим в правой части слагаемое вида , где составляющие его сомножители имеют вид (формулы (67), (75) в работе [14]):

                                            ;                              (17)

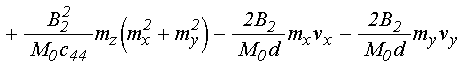              .      (18)

 

Выполняя умножение, подставляя полученное произведение в продифференцированное по времени выражение (3) и оставляя только члены, существенные для настоящего рассмотрения, для компоненты намагниченности  получаем уравнение:

,                                   (19)

 

где  является слагаемым связи   с другими компонентами намагниченности и представляет собой многочлен, содержащий произведения всех трех компонент вектора намагниченности во всех степенях, начиная с первой и кончая девятой. Таким образом, обсуждаемое далее соотношение  2, 4, 6, 7 и последующих степеней намагниченности в первом уравнении с первой степенью во втором, выполняется, что и доказывает для магнитоупругой системы возможность существования автомодуляционных колебаний.  

Подобное рассмотрение системы, состоящей из магнитного и электродинамического резонаторов [21-23], приводит к тем же результатам. Главной причиной, обусловливающей возможность автомодуляционных колебаний в подобных системах, является наличие нелинейного магнитного или сходного по свойствам резонатора, в котором связь с другим резонатором является нелинейной по амплитуде колебаний обоих резонаторов. В магнитном случае это обеспечивается наличием в уравнении для  слагаемых вида  и аналогичных слагаемых в двух других уравнениях. 

 

3. Модель связанных линейного и нелинейного осцилляторов

Общий характер рассматриваемых задач позволяет сформулировать модель, содержащую максимально простой вид связи, при котором еще возможны колебания автомодуляционного характера. В настоящей работе в качестве такой модели была принята система из двух связанных осцилляторов, из которых первый является нелинейным (аналог магнитного резонатора), а второй – линейным (аналог электродинамического или упругого резонатора). Связь между осцилляторами предполагается невзаимной и нелинейной. Возбуждающая сила действует только на первый нелинейный осциллятор. Рассматривалось развитие колебаний обоих осцилляторов во времени после включения возбуждения.

В качестве такой наиболее простой модели была рассмотрена следующая система уравнений:

;     (20) 

.                                  (21) 

 

Здесь , ,  – координатные переменные, параметры затухания и собственные частоты осцилляторов,  – коэффициенты связи,  – параметр нелинейности первого осциллятора,  и   – амплитуда и частота возбуждающей силы,  –  показатели степени слагаемого связи.  

Поставленная так задача решалась численно методом Рунге-Кутта четвертого порядка [32].      

В ходе исследований было выявлено, что приведенная система уравнений допускает автомодуляционное решение при следующих условиях: связь во втором уравнении всегда должна быть первой степени, а в первом – второй, четвертой, шестой и всех последующих степеней (2,4,6,7,8,9,…). Условия возбуждения к подбору параметров довольно критичны. Наиболее легко автомодуляционные колебания получаются при сочетании: , , так что ограничимся далее именно этим случаем.  

В работах [19,20] в подобных условиях были выявлены два вида автомодуляционных колебаний – синхронный и асинхронный.  

Однако параметры решенной там задачи были заданы случайным образом, что не позволило судить о наблюдаемых явлениях с достаточной общностью. Рассмотрим здесь разнообразие возникающих колебаний более подробно.

 

4. Нелинейная связь между линейными осцилляторами

Сначала обратимся к случаю, когда оба осциллятора являются линейными, а связь между ними – нелинейна, то есть в уравнениях (20)-(21) будем полагать: . Для простоты рассмотрения зададим параметры задачи небольшими целыми числами, что, не ограничивая общности, позволяет избежать необходимости сравнения величин высоких порядков, в то же время повышая наглядность и создавая удобства для машинного счета. При этом фактическую размерность параметров будем опускать, полагая все расчеты выполненными в соизмеримых единицах. Так положим частоты обоих осцилляторов, а также частоту возбуждения равными друг другу:  Параметры затухания также положим одинаковыми:  Также зададим равными параметры связи:  Таким образом, осцилляторы можно считать идентичными, кроме связи, которая для первого осциллятора относительно второго является квадратичной, а для второго относительно первого – линейной.

Предварительное исследование показало, что все наблюдавшиеся в настоящей работе режимы вынужденных колебаний можно было реализовать путем изменения в достаточно широких пределах только амплитуды возбуждения.  

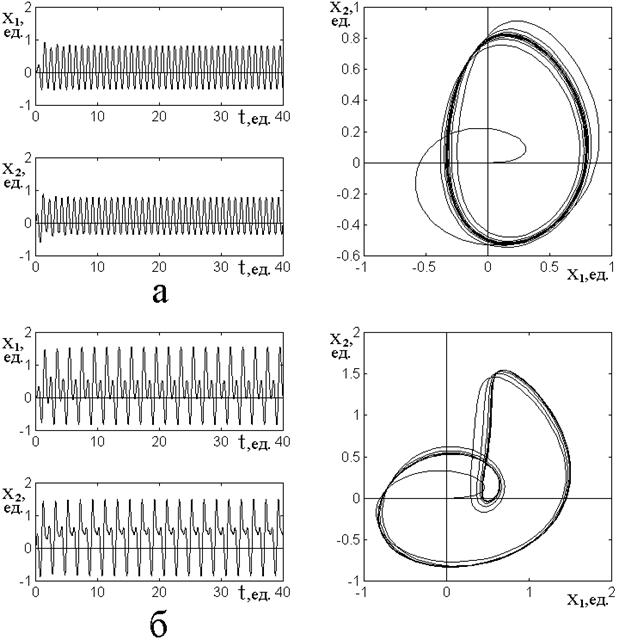
Примеры получаемых при этом режимов колебаний иллюстрируются рис.2. Рассмотрим трансформацию колебаний при последовательном увеличении  возбуждения более подробно.

При уровне возбуждения ниже  – колебания полностью регулярны, имеют вид правильных синусоид, параметрический портрет представляет собой четко выраженное узкое кольцо.

При увеличении возбуждения выше  синусоидальная правильность формы колебаний слегка нарушается, в результате чего образующая параметрического кольца начинает слегка размываться, как это показано на рис.2а.   

При увеличении возбуждения выше  синусоида колебаний начинает расщепляться, то есть между основными колебаниями появляются отщепленные колебания меньшей амплитуды, как это показано на левых эпюрах рис.2б. При этом полный период колебаний как бы удваивается, в результате чего кольцо разделяется по ширине на два четких вложенных друг в друга кольца, которые при возбуждении выше  разъезжаются в стороны, образуя в области своего перекрытия петлю, как это видно из рис.2б. Размер петли, сначала близкий к размеру исходного кольца, вследствие уменьшения перекрытия образовавшихся колец, постепенно уменьшается вплоть до нуля, в результате чего петля при уровне возбуждении около  полностью разглаживается. При этом общее кольцо снова становится единым, приобретая вид выпукло-вогнутой «чечевицы», с четкой огибающей, напоминающей зерно фасоли.

 

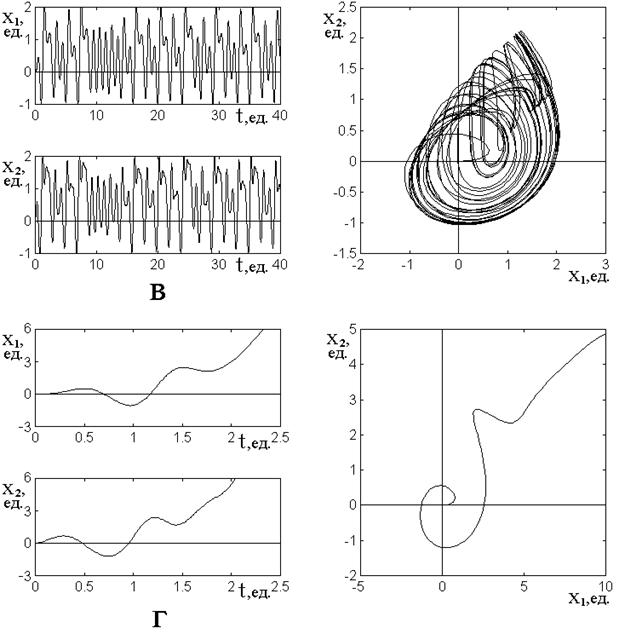
Рис.2. Режимы колебаний при различной величине возбуждения. Слева – развертки колебаний во времени, справа – параметрические портреты.

Амплитуда возбуждения: а – ;   б – ;    в – ;   г – .

 

При увеличении возбуждения выше  четкий периодический характер колебаний нарушается, появляются отдельные сбои периода, постепенно распространяющиеся на все времена. Характер колебаний теряет регулярность, приобретая элементы хаотичности (рис.2в). При этом огибающая чечевицы сначала начинает расщепляться, а при дальнейшем увеличении возбуждения все более размазывается, в результате чего чечевица практически полностью замывается уже при уровне возбуждении равном  

При дальнейшем увеличении возбуждения характер колебаний остается нерегулярным вплоть до , после чего колебания срываются и координатные переменные обоих осцилляторов устремляются к бесконечности (рис.2г).  При этом параметрическая чечевица сменяется единственной изогнутой линией, также уходящей на бесконечность. Такой переход от замкнутой чечевицы к расходящейся кривой имеет резкий порог, равный  (с точностью до ).  

 

5. Основные режимы вынужденных колебаний

Из описанного характера вынужденных колебаний можно выделить пять характерных режимов.

Режим №1 – регулярный синусоидальный.

Имеет место при  . Характеризуется четкими регулярными колебаниями обоих осцилляторов, имеющими правильный синусоидальный характер. Параметрический портрет имеет вид правильного узкого кольца близкой к круговой формы. 

Режим №2 – регулярный с расщеплением.

Имеет место при . Характеризуется отщеплением от каждого полупериода синусоиды небольшого дополнительного пика, отделенного от основного минимумом. Колебания остаются регулярными, приобретая вид наложенных друг на друга двух синусоид с разными амплитудами. Общий период колебаний удваивается. Параметрический портрет имеет форму двух частично перекрывающихся колец, образующих в области перекрытия замкнутую петлю.

Режим №3 – регулярный без расщепления.   

Имеет место при . Характеризуется также отщеплением от каждого полупериода синусоиды дополнительного пика, однако минимум между основным и дополнительным пиками постепенно сглаживается. Общий период остается удвоенным. Параметрический портрет имеет форму единого кольца имеющего вид выпукло-вогнутой чечевицы, петля полностью отсутствует.

Режим №4 – нерегулярный квазихаотический.

Имеет место при . Характеризуется скачкообразным изменением амплитуды синусоиды от периода к периоду. Колебания теряют четкую периодичность, хотя в среднем перемена их полярности во времени остается близкой к исходной. Изменение амплитуды носит квазихаотический характер. Огибающая параметрического портрета имеет вид выпукло-вогнутой чечевицы, полностью замазанной случайно блуждающими траекториями.

Режим №5 – нерегулярный расходящийся.

Имеет место при . Характеризуется несколькими (одним-двумя) возвратно-поступательными колебаниями, переходящими в стремление переменных к бесконечности. Параметрический портрет имеет вид раскручивающейся спирали,  после нескольких (одного-двух) витков уходящей на бесконечность.

Переходы между режимами №1-№4 по амплитуде возбуждения являются довольно плавными (в пределах  от средней величины), то есть беспороговыми. Переход между режимами №4 и №5 имеет резкий порог (менее  от средней величины).

Замечание. Из сравнения с результатами работы [19] можно видеть, что описанные там колебания, названные «синхронными» (рис.1 в работе [19]), содержат в себе элементы регулярного режима с расщеплением №3 (четко выраженные минимумы между основными и дополнительными пиками), регулярного режима без расщепления №4 (отсутствие петли, ярко выраженная чечевица) и даже в какой-то степени нерегулярного режима №5 (частичное размазывание чечевицы). Надо полагать, что такое разнообразие обусловлено с одной стороны довольно специфическим выбором параметров осцилляторов (частоты, параметры затухания и связи различны, связь весьма велика: , , , , , , , , , , ), и с другой – отсутствием четко выраженных границ между режимами с частичным перекрытием между ними, отмеченным здесь даже для идентичных осцилляторов.     

  

6. Нелинейность первого осциллятора

В рамках рассматриваемой задачи о магнитоупругих колебаниях ферритовой пластины (разделы №1-№3), магнитный осциллятор является нелинейным, а упругий – линейным. Рассмотрим теперь роль нелинейности первого осциллятора при условии сохранения линейности второго. Связь между осцилляторами оставим прежней, то есть в уравнениях (20)-(21) положим , . Нелинейность введем в уравнение (20) посредством отличного от нуля параметра  при третьей степени .

Предварительное исследование показало, что введение такой нелинейности при  приводит преимущественно к регуляризации колебаний обоих осцилляторов, то есть преобладающим становится режим №1. При довольно высоком уровне возбуждения (более ) режим №1 переходит в режимы №3 и №4, но при дальнейшем увеличении возбуждения характер колебаний снова приближается к режиму №1. При достаточно большой величине  (более ) режим №5 также не реализуется, то есть система не уходит на бесконечность ни при каком сколь угодно большом уровне возбуждения. Реализация режима №4, то есть нерегулярных квазихаотических колебаний, становится по параметрам довольно критичной, причем с увеличением нелинейности критичность возрастает.

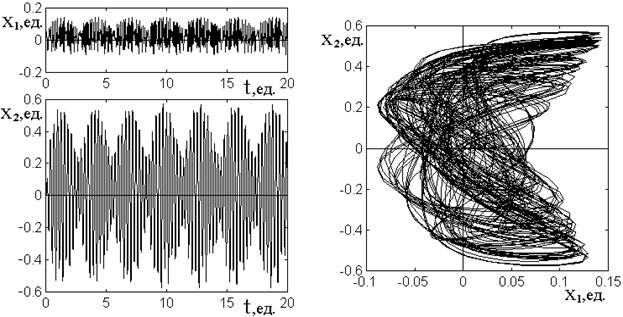
Типичный пример колебаний при умеренном уровне нелинейности показан на рис.3.

Первыми характерными особенностями наблюдаемой картины являются значительно (примерно в два раза) меньшая амплитуда и резкое (в три-пять раз) уменьшение периода колебаний первого осциллятора по сравнению с амплитудой и периодом колебаний второго. Причиной этих двух особенностей является именно нелинейность первого осциллятора, то есть они проявляются, начиная примерно с , тем сильнее, чем параметр  больше. К остальным параметрам эти особенности не критичны, то есть сохраняются при изменении упомянутых параметров в обе стороны не менее чем на порядок. 

 

Рис.3. Колебания при нелинейности первого осциллятора. Слева – развертки колебаний во времени, справа – параметрический портрет.

Параметры: ,  , , ,  .

 

Далее можно видеть, что колебания обоих осцилляторов, особенно второго, близки к регулярным с расщеплением (режим №3), однако расщепление здесь происходит для второго осциллятора не на два пика, а на три, а для первого – на еще большее их количество (пять-семь). Кроме того, повторяемость колебаний от периода к периоду для второго осциллятора хотя и в общем соблюдается, тогда как для первого сильно нарушена. Параметрический портрет имеет множественный сильно расщепленный характер, главным образом за счет нерегулярности колебаний первого осциллятора, то есть в колебаниях явно присутствуют элементы нерегулярной квазихаотичности, характерной для режима №4.

Такой смешанный регулярно-квазихаотический режим к выбору параметров довольно критичен. Так при уменьшении параметра нелинейности с  до  Колебания становятся регулярными, то есть наступает режим №1 с едва заметными элементами расщепления, которые при уменьшении  до  пропадают. То же происходит при уменьшении параметров связи с  до  Увеличение параметра нелинейности выше  или параметров связи выше  элементы квазихаотичности устраняет, однако расщепление остается вплоть до , после чего колебания опять стремятся к регулярности.

Важно отметить, что при  увеличение возбуждения до сколь угодно большого уровня к расходимости (режиму №5) не приводит. При этом более или менее устойчиво реализуется режим №3, причем амплитуда отщепленных импульсов приближается к амплитуде основного, а кратность расщепления особенно для первого осциллятора возрастает (при  становится больше десятка), то есть колебания превращаются в регулярную последовательность почти прямоугольных импульсов с сильно изрезанной плоской частью.

По амплитуде возбуждения наблюдаемые автомодуляционные колебания имеют довольно заметно выраженный порог. Переход от  регулярного режима №1 к регулярному с расщеплением №2 происходит при . При увеличении затухания любого из осцилляторов в несколько (3-5) раз этот порог повышается, примерно пропорционально степени увеличения затухания. При увеличении затухания обоих осцилляторов на порядок автомодуляционные явления не наблюдаются и колебания остаются близкими к регулярным, в том числе при настолько большой нелинейности (), что переход к режиму №5 не имеет места.   

 

7. Асинхронные колебания

Проведенное выше рассмотрение относится к случаю одинаковых параметров обоих осцилляторов. Однако в реальном случае магнитоупругих колебаний параметры осцилляторов сильно различаются. Так параметр затухания магнитного осциллятора, как правило, значительно выше параметра затухания упругого. Магнитный осциллятор является сильно нелинейным, тогда как упругий – полностью линейный. Собственные частоты осцилляторов могут отличаться друг от друга, а частота возбуждения может отличаться от обеих этих частот. Связь между осцилляторами является нелинейной и довольно сильной.

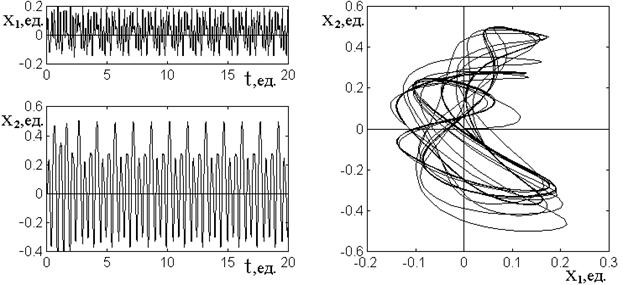
В работах [19,20] показано, что в таких условиях в системе может существовать особый вид автомодуляционных колебаний, период которых значительно (в несколько раз) больше периода возбуждающей силы. Такие колебания там названы «асинхронными». Иллюстрацией асинхронных колебаний осцилляторов в случае сильного различия между ними является рис.4, для удобства сравнения построенный при параметрах, сходных с таковыми в работе [19].

 

Рис.4. Асинхронные колебания при неидентичности осцилляторов. Слева – развертки колебаний во времени, справа – параметрические портреты.

Параметры:  (),  (),  (), , , , , , .

 

Характерной особенностью наблюдаемой картины является значительно (в три-четыре раза) меньшая амплитуда колебаний первого осциллятора по сравнению с амплитудой колебаний второго. Такая особенность наблюдалась и в случае идентичных осцилляторов (раздел №6) и также обусловлена нелинейностью первого из них.

Главной особенностью асинхронных колебаний является их двухпериодичность. Так колебания второго осциллятора имеют четко выраженные два периода. Первый из них – малый, равен  и соответствует периоду возбуждения, второй – большой, равен  и определяется параметрами осцилляторов. Колебания первого осциллятора также имеют четко выраженный период, равный , то есть большому периоду колебаний второго осциллятора. Эта периодичность особенно ярко проявляется на верхней огибающей развертки колебаний, на нижней же ее роль менее заметна. Внутри такого периода колебания имеют близкий к хаотическому характер, малая периодичность в котором выражена значительно слабее, однако все же ее проявление в какой-то степени имеет место. Длительность такого малого внутреннего «квазипериода» близка к длительности периода возбуждения.

Перечисленные особенности позволяют выделить асинхронные колебания в особый режим.

Режим №6 – асинхронный.

Имеет место при значительном отличии параметров осцилляторов друг от друга. Характеризуется двухпериодичностью колебаний, малый период которых совпадает с периодичностью возбуждения, а большой – превышает период возбуждения в несколько раз. Изменение амплитуды второго осциллятора носит периодический характер, типичный для случая синусоидальной амплитудной модуляции единственной частотой, определяющей величину большого периода. Изменение амплитуды первого осциллятора по большому периоду синхронно с таковым для второго осциллятора, а внутри малого периода носит квазихаотический характер. Параметрический портрет заметно размазан за счет хаотической составляющей колебаний первого осциллятора.

Рассмотрим особенности асинхронного режима с точки зрения критичности параметров осцилляторов и возбуждения.

Основной (большой) период асинхронных колебаний от амплитуды возбуждения и значений параметров затухания обоих осцилляторов зависит довольно мало: меняется не более чем на  при изменении тех и других на порядок. Заметная зависимость периода наблюдается от соотношения собственных частот осцилляторов друг с другом и частотой возбуждения. Так при увеличении частоты второго осциллятора с  до  период уменьшается примерно в полтора раза, а при дальнейшем увеличении этой частоты амплитуда асинхронных колебаний падает в три-пять раз и режим приближается к регулярному.

При равенстве частот обоих осцилляторов величине  и сохранении частоты возбуждения  асинхронные колебания сильно хаотизируются, четко выраженный период исчезает и режим приближается к нерегулярному квазихаотическому №4. При равенстве частот обоих осцилляторов друг другу и частоте  возбуждения  асинхронные колебания пропадают и режим приближается к регулярному №1.

К параметру нелинейности  колебания становятся критичными только при его значительном уменьшении. Так при изменении  от до  период и амплитуда асинхронных колебания меняются не более чем на . Однако в нижней части этого диапазона глубина модуляции асинхронных колебаний уменьшается с  при  до  при  При уменьшении  до  четко выраженный период пропадает, колебания слегка хаотизируются, а при дальнейшем уменьшении  до  система уходит на бесконечность, то есть реализуется режим №5.

К параметрам связи  колебания мало критичны в интервале от до Период меняется мало (не более ), однако вблизи нижней границы этого интервала глубина модуляции уменьшается до , а при дальнейшем уменьшении связи колебания регуляризируются, то есть наступает режим №1. При увеличении параметров связи выше вплоть до четкая периодичность асинхронных колебаний нарушается, период с течением времени скачкообразно меняется в два-три раза и более, хотя глубина модуляции сохраняется близкой к . Дальнейшее увеличение параметров связи до приводит к переходу системы в новое стационарное состояние: колебания полностью регуляризируются, их частота равняется частоте возбуждения, а амплитуда резко падает,  отклонение первого осциллятора от нуля составляет около , а второго –  При этом амплитуда колебаний первого осциллятора не превышает , а второго –  То есть происходит явление, подобное переориентации вектора намагниченности в нормально намагниченной ферритовой пластине при изменении параметра магнитоупругой связи [33].   

По амплитуде возбуждения асинхронные колебания имеют хорошо выраженный порог. Переход от  регулярного режима №1 асинхронному происходит при  При увеличении затухания любого из осцилляторов в несколько (3-5) раз этот порог незначительно (не более полутора раз) повышается. При увеличении затухания обоих осцилляторов до  автомодуляционные явления не наблюдаются и колебания остаются близкими к регулярным (режим №1). 

 

8. Модель обобщенного потенциала

Предложенная модель связанных линейного и нелинейного осцилляторов, описываемая системой уравнений (20)-(21), несмотря на свою схематичность, позволяет выявить основные свойства автоколебаний магнитоупругой и магнито-электродинамической систем, такие как пороговый характер, роль параметров затухания и нелинейности осцилляторов и связи, переход к стохастическому режиму при большом уровне возбуждения.

Однако выполненное исследование системы (20)-(21) имеет в первую очередь отвлеченный математический смысл до тех пор, пока в основу ее интерпретации не будет положена реальная физическая модель.

В традиционной трактовке многих задач о колебаниях часто используется модель потенциальной ямы (или «ящика»), вблизи минимума которого частица совершает периодические колебания [34,35].  

Рассмотрим модель обобщенного потенциала, которую можно положить в основу физической интерпретации описанных колебательных явлений.  

Будем полагать, что система уравнений движения для осцилляторов имеет вид:

;                                           (22)

 ,                                                          (23)

 

где  – обобщенный потенциал системы в целом, а третьи слагаемые представляют собой обобщенные силы (знак для удобства учтен заранее). Диссипативные члены в этот потенциал не включены, чтобы не усложнять вычисления.

Согласно общей трактовке задачи о связанных магнитном и упругом (или магнитном и электродинамическом) осцилляторах (раздел №3), обобщенный потенциал должен содержать слагаемые вида , где   и  – целые числа от 0 до 9. В работах [24-27] показано, что связь между магнитным и упругим осцилляторами может осуществляться также за счет производных от переменных по координатам, однако такую связь пока рассматривать не будем. Ограничимся также степенью входящих в потенциал переменных не выше четвертой. В таких предположениях обобщенный потенциал принимает вид:

,                                                      (24)

где

;                                                                         (25)

;                                                         (26)

;                                         (27)

.                        (28)

Из этих выражений обобщенные силы получаются путем дифференцирования по переменным . Очевидно, что первое выражение (25) дает статическую постоянную силу, которая на колебаниях никак не сказывается, так что можно заведомо положить , то есть .

Второе выражение (26) дает в уравнениях линейные слагаемые, пропорциональные , то есть собственные частоты осцилляторов  в линейном приближении, а также линейные связи между ними. Таким образом, можно положить: , , а также , где  – параметр линейной связи между осцилляторами, который должен в одинаковой степени присутствовать в обоих уравнениях.  

Третье выражение (27) дает прежде всего параметры квадратичной нелинейности для обоих осцилляторов через слагаемые с  и . Однако квадратичная нелинейность, не будучи дополненной нелинейностью более высоких порядков, вызывает уход системы на бесконечность вследствие нечетности потенциала каждого из осцилляторов по отдельности, то есть при отрицательном значении переменной вследствие стремления энергии к минимуму система устремляется на минус бесконечность по спадающей ветви кубической параболы, перегиб которой приходится на нуль. Таким образом, для исключения расходящихся решений в отсутствие связи между осцилляторами, следует положить .

Другие два слагаемых дают силы для первого осциллятора пропорциональные  и , а для второго – тоже , а также . Первые из этих пар слагаемых обеспечивают нелинейную связь между осцилляторами низшего порядка, которая в силу своей нечетности также может привести к расходимости. Вторые же слагаемые обеспечивают квадратичную связь, однако не будучи дополненными слагаемыми более высокого порядка также могут увести систему на бесконечность вследствие нечетности потенциала.  

Четвертое выражение (28) дает прежде всего параметры кубической нелинейности для каждого из осцилляторов через слагаемые с  и . Потенциал в этом случае является четным, что уход на бесконечность полностью исключает. При достаточной величине констант  и  такая четность четвертого порядка может компенсировать нечетность более низких порядков, в частности, третьего, то есть предотвратить уход на бесконечность, обеспечиваемый слагаемыми, составляющими выражение (27).   

Остальные слагаемые выражения (28) дают различные виды нелинейной связи между осцилляторами, такие как  и , входящие в то или иное уравнение. Кроме того они могут дать кубические виды связи для первого уравнения вида  и для второго вида .

Заметим, что здесь, хотя в потенциале (24) и присутствуют слагаемые третьей степени по обеим переменным, но эти слагаемые входят наряду со слагаемыми более низких степеней, поэтому у получающихся кубических парабол могут иметься локальные минимумы (то есть соответствующее кубическое уравнение имеет три действительных корня). По одну сторону от такого минимума кубическая парабола уходит на плюс бесконечность, а по другую идет вверх до определенного локального максимума – потенциального барьера, достигая который и переваливая через него устремляется к минус бесконечности. Таким образом, в окрестности локального минимума могут происходить колебания с ограниченной амплитудой, а при превышении амплитуды над потенциальным барьером система уходит на бесконечность. Заметим, что подобное свойство кубического потенциала в сочетании с потенциалом четвертой степени, дающее малые локальные колебания с уходом на бесконечность при превышении определенного порога, в классике хорошо известно и проявляется, например, в уравнении Дуффинга [35].

Возвращаясь к рассмотрению системы (20)-(21) можно видеть, что в полном выражении для потенциала (24)-(28) главную роль играют во-первых, слагаемые с коэффициентами  и , дающие собственные частоты осцилляторов, во-вторых – во втором уравнении – слагаемое с , обеспечивающее линейную связь второго осциллятора с первым. Заметим, что в первом уравнении такое слагаемое отсутствует, однако контрольная проверка показывает, что роль его в сравнении со слагаемым квадратичной связи довольно невелика и характера рассмотренных колебаний практически не меняет.

Далее важно слагаемое с , ответственное за кубическую нелинейность первого осциллятора, а также слагаемое с , обеспечивающее квадратичную связь первого осциллятора со вторым. Все остальные слагаемые в настоящем рассмотрении можно положить равными нулю. Определенную роль может играть также слагаемое с , дающее в первое уравнение вклад вида , однако проверка показывает, что общий характер колебаний при учете такого слагаемого не меняется. 

Таким образом, обращаясь к соответствию между выражениями (24)-(28) и системой уравнений (20)-(21) получаем:

;                                                                                         (29)

;                                                                                         (30)

;                                                                                            (31)

;                                                                     (32)

 (или ).                                                                    (33)

 

При таком наборе параметров потенциал (24) принимает вид:

.                               (34)

Здесь первое и третье слагаемые определяют собственные частоты осцилляторов, второе – линейную связь между ними, четвертое – нелинейность первого осциллятора, пятое – нелинейную связь между осцилляторами.

В соответствии с физической природой входящих в (34) коэффициентов (то есть в соответствии с (29)-(33)), все их надо считать положительными.

Важно отметить, что первые четыре слагаемых потенциала являются четными по степеням переменных (степени вторая и четвертая), тогда как пятое – нечетным (степень – третья). При этом из четных, независящими от знаков переменных, являются только слагаемые с коэффициентами ,  и , то есть вклад этих слагаемых в общий потенциал всегда положителен. Однако слагаемое с коэффициентом  положительно только при одинаковых знаках обеих переменных, а при одном из них отрицательном может дать в потенциал отрицательный вклад. Знак слагаемого с коэффициентом  от знака  не зависит, однако он положителен только при  положительном значении , а при отрицательном – его вклад в потенциал также отрицателен. Физические следствия такого характера знаков слагаемых потенциала будут рассмотрены в следующем разделе.  

Получаемые из потенциала (34) обобщенные силы имеют вид (отрицательные знаки перед производными присутствуют также и в уравнениях, то есть взаимно уничтожаются, поэтому здесь для простоты опущены): 

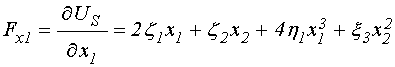;                                (35)

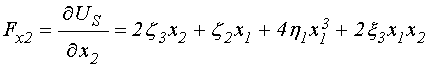.                         (36)

 

Уравнения принимают вид:

;  (37)

.                         (38)

 

Эта система имеет довольно общий характер. Здесь в первом уравнении присутствует кубическая нелинейность (через посредство ), тогда как во втором подобная нелинейность отсутствует. В обоих уравнениях присутствует линейная связь с другим уравнением (через ). Во втором уравнении присутствует квадратичная связь с первым вида , то есть по второй переменной  связь является линейной. Таким образом, эта система имеет основные признаки рассмотренной в разделе №3 системы (20)-(21), такие как кубическая нелинейность по первой переменной, квадратичность связи в первом уравнении и линейность во втором. То есть в некотором отношении систему (20)-(21) можно считать частным случаем полученной здесь на основе модели обобщенного потенциала системы (37)-(38).

Замечание. Следует заметить, что системы (20)-(21) и (37)-(38) полностью тождественными не являются, то есть при простой замене коэффициентов вида (29)-(33) одна в другую не переходят. В системе (37)-(38) имеются отличия от (20)-(21), такие как линейная связь с одним и тем же коэффициентом в обоих уравнениях ( и ), а также во втором уравнении умножение линейной связи по первой переменной на вторую переменную (вида ). Однако предварительное исследование не выявило решающего влияния этих отличий на характер поведения системы в целом, поэтому их более подробное рассмотрение в настоящей работе проведено не было, хотя и предполагается в дальнейшем.

 

9. Применение модели потенциала к интерпретации характера колебаний

Применим теперь предложенную модель обобщенного потенциала к интерпретации вынужденных колебаний системы связанных осцилляторов при различных уровнях возбуждения, степени нелинейности и характере связи. 

Прежде всего отметим, что входящие в уравнения (37)-(38) первые два слагаемых, содержащие вторую и первую производные по времени, отражают обычные свойства колебаний, такие как периодичность и затухание во времени, то есть с моделью потенциала напрямую не связаны. Все остальные слагаемые, содержащие переменные в различных сочетаниях, определяются уже непосредственно потенциалом, поэтому рассмотрим роль его слагаемых по отдельности. 

Обратимся к рис.5, где показаны различные варианты формы потенциальной поверхности, построенной по формуле (34) в координатах  (точка  соответствует началу координат , ,  и для удобства рисунка явно не обозначена). На горизонтальной плоскости  приведены эквипотенциальные линии, то есть сечения потенциальной поверхности горизонтальной плоскостью, соответствующие некоторым характерным значениям потенциала. 

 

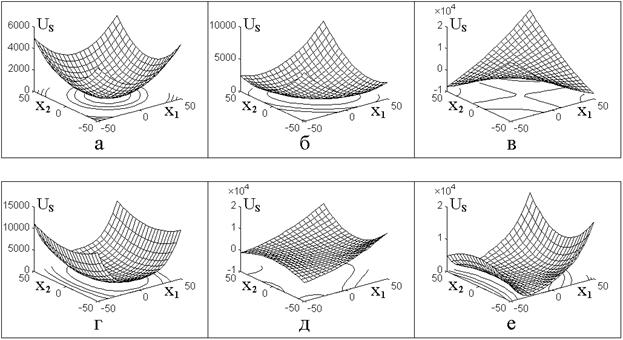
Рис.5. Потенциальные поверхности при различных параметрах связи и нелинейности осцилляторов.

а – связь отсутствует, оба осциллятора линейные;

б – линейная связь слабая, оба осциллятора линейные;

в – линейная связь сильная, оба осциллятора линейные;

г – связь отсутствует, первый осциллятор – нелинейный, второй – линейный;

д – связь по первому осциллятору квадратичная, оба осциллятора линейные;

е – связь по первому осциллятору квадратичная, первый осциллятор – нелинейный, второй – линейный;

 

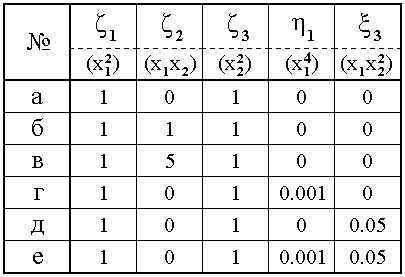
Наборы коэффициентов, использовавшихся при построении рис.5а-5е, приведены в таблице 1. Собственные частоты осцилляторов полагаются равными друг другу, причем для простоты положены равными единице. Все остальные числовые значения коэффициентов выбраны из условия наглядности построения.

 

Таблица 1. Коэффициенты построения потенциальных поверхностей.

 

Проводя механическую аналогию, колебания можно рассматривать как периодическое «катание шарика» по потенциальной поверхности при условии действия направленной вниз силы тяжести. Рассмотрим различные варианты такого «катания» по отдельности. 

Рис.5а соответствует набору «а» в таблице 1. В этом случае осцилляторы никак не связаны. Потенциальная поверхность является симметричной относительно вертикальной оси. Эквипотенциальные кривые представляют собой правильные окружности. Для каждого осциллятора возможны периодические колебания с ограниченной амплитудой, от колебаний другого осциллятора полностью независимые. При этом, поскольку первый осциллятор возбуждается периодической силой, то в установившемся режиме он колеблется с постоянной амплитудой, тогда как колебания второго возможны только при каком-то начальном отклонении и во времени имеют затухающий характер.

Рис.5б соответствует наличию слабой линейной связи между осцилляторами, определяемой коэффициентом . При этом потенциальная поверхность слегка вытягивается вдоль линии, соответствующей , составляющей с осями  и  углы по . На этой линии у поверхности появляются широкие «крылья», формирующие продольную «лощину». Эквипотенциальные кривые представляют собой вытянутые эллипсы, большая ось которых ориентирована вдоль упомянутой линии. Колебания осцилляторов синхронизируются друг с другом, будучи сдвинутыми по фазе на . Это – классическая картина связанных колебаний двух осцилляторов при линейной связи [36,37]. Такие колебании я соответствуют рассмотренному в разделе №5 режиму №1 (регулярный синусоидальный). На сдвиг фазы на  между колебаниями магнитного и упругого осцилляторов указывалось также в работах [14-16, 24-28], посвященных нелинейному возбуждению гиперзвука. 

Рис.5в соответствует наличию сильной линейной связи между осцилляторами, определяемой коэффициентом . При этом «крылья» потенциальной поверхности склоняются вниз, так что вместо «лощины» появляется «седло». Эквипотенциальные кривые представляют собой гиперболы, обращенные вершинами друг к другу, с осями симметрии, соответствующими . Переход от «лощины» на рис.5б к «седлу» на рис.5в, то есть от случая «слабой» связи к «сильной» происходит при критическом значении параметра . 

Периодические колебания при таком потенциале невозможны: система при любом сколь угодно малом отклонении от нуля «скатывается вниз» по боковым поверхностям «седла», что проявляется как уход переменных  и  на бесконечность.

Подобное поведение системы отмечалось в разделе №5, как свойственное режиму №5 (нерегулярный расходящийся). Уход на бесконечность отмечался также в работе [27], как эквивалент переориентации вектора намагниченности в нормально намагниченной пластине при достаточной величине константы магнитоупругой связи  (рис.5д,е в работе [27]). Подобная переориентация, вызванная значительной величиной той же константы, подробно разбиралась в работе [33]. Во всех этих случаях можно полагать объяснение наблюдаемой расходимости с помощью модели потенциала достаточно адекватным. 

Рис.5г соответствует отсутствию связи между осцилляторами, но наличию кубической нелинейности первого осциллятора, определяемой коэффициентом . Потенциальная поверхность по обеим переменным является симметричной в силу четности соответствующих слагаемых выражения (34). Рост потенциала  по мере увеличения  становится более значительным, чем на рис.5а, тогда как по  остается прежним. В результате потенциальная поверхность приобретает вид «лощины», вытянутой вдоль оси , а эквипотенциальные кривые обращаются в эллипсы с большой осью, ориентированной вдоль той же оси. Колебания каждого из осцилляторов по отдельности, как и в случае рис.5а, возможны и имеют периодический характер. Потенциал всегда остается четным, поэтому какая-либо расходимость отсутствует.

Рис.5д соответствует наличию между осцилляторами нелинейной связи, задаваемой коэффициентом , тогда как сами осцилляторы остаются линейными. В этом случае потенциальная поверхность относительно переменной  является симметричной вследствие квадратичности этой переменной в пятом слагаемом потенциала (34). Симметрия относительно переменной  становится центральной с двойной кратностью, то есть при изменении знака  добавка к потенциалу становится отрицательной. Это проявляется в загибе вниз обоих углов поверхности при  (на рисунке при ). Эллипсы эквипотенциальных кривых при отрицательных значениях  разрываются, формируя гиперболы с ветвями, стремящимися к бесконечности. 

Такой разрыв эллипсов с загибом углов поверхности вниз происходит только при достаточной величине коэффициента , так как ему надо преодолеть загибы углов вверх, определяемые коэффициентом  (рис.5а). Поэтому при малых значениях  колебания в системе имеют ограниченный характер, подобный режиму №1. Однако, благодаря наличию при коэффициенте  квадрата переменной , при достаточной величине этой переменной отрицательный вклад слагаемого с  может пересилить положительный вклад от слагаемого с . В этом случае потенциальная поверхность в начальной точке системы координат приобретает седловидный характер, так что периодические колебания в такой системе опять становятся невозможными, то есть система, скатываясь по боковым склонам «седла», уходит на бесконечность. 

Итак, в случае умеренных значений коэффициента  при малом уровне возбуждения колебания в системе остаются периодическими, тогда как при большом его уровне система уходит на бесконечность. В разделе №5 такое поведение системы проявляется как последовательный переход при увеличении уровня возбуждения от режима №1 через режимы №2 и №3 к режиму №4 и далее к режиму №5. 

Рис.5е соответствует наличию между осцилляторами нелинейной связи, задаваемой коэффициентом , в сочетании в кубической нелинейностью первого осциллятора, задаваемой коэффициентом . Можно видеть, что загибы углов поверхности вниз, характерные для рис.5д, здесь в значительной степени компенсированы стремлением тех же углов вверх, подобным показанному на рис.5г. Такая компенсация происходит из-за четности потенциала при коэффициенте , причем здесь степень этой четности равняется четырем, тогда как степень нечетности при коэффициенте  составляет всего три. Такая четность, преобладая над нечетностью вследствие своей более высокой степени, формирует минимум на потенциальной поверхности, в пределах которого колебания остаются конечными при любом сколь угодно высоком уровне возбуждения. Эквипотенциальные кривые при этом снова замыкаются, причем их форма, хотя и отличается от эллиптической, напоминая треугольную со закругленными углами, но всегда при этом остается замкнутой.  

Такая компенсирующая роль кубической нелинейности первого осциллятора отмечена в разделе №6 при рассмотрении рис.3. Там же отмечено, что колебания, хотя и остаются периодическими с конечной амплитудой, но их форма приближается к прямоугольной. Здесь же причиной такой особенности можно считать искажение эллиптической формы эквипотенциальных кривых с ее стремлением к треугольной. 

Заметим, что роль кубической нелинейности в компенсации расходимости колебаний системы двух осцилляторов отмечалась также в работе [27, рис.6], где рассматривалось развитие колебаний во времени. Можно полагать, что рассматриваемая здесь модель обобщенного потенциала применима и к этому случаю в достаточной мере.

 

10. Модель расщепления синусоиды

В предыдущем разделе показано, что модель потенциала, в зависимости от соотношения коэффициентов, позволяет интерпретировать периодический характер колебаний, а также  уход системы на бесконечность по достижении определенного порога. То есть выявлены основные свойства режимов №1 и №5. Режимы №2, №3 и №4 при этом положены развитием режима №1 до наступления режима №5. Однако природа свойственного режимам №2-№4 расщепления синусоидальных колебаний остается невыясненной.

Покажем здесь, что такое расщепление может явиться следствием возбуждения второй гармоники основных колебаний за счет нелинейности системы. Иллюстрацией тому является рис.6, где слева представлены развертки по времени колебаний первого и второго осцилляторов, а справа – соответствующий параметрический портрет. Развертки колебаний построены с помощью формул:

;                                                                                   (39)

,                                                                        (40)

где коэффициенты выбраны минимально необходимыми для выявления существа явления.

 

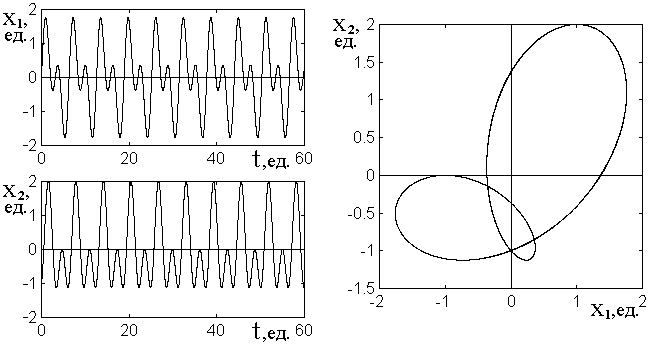
Рис.6. Иллюстрация роли возбуждения второй гармоники колебаний.

 

Видно, что в обоих случаях за счет второй гармоники имеет место удвоение периода, характерное для разверток, представленных на рис.2б, то есть для режима №2. Параметрический портрет имеет петлю, подобную проявляющейся на рис.2б, тоже характерную для режима №2.  

Нелинейность системы, требуемая для появления двойной частоты, может быть обусловлена как нелинейностью любого из осцилляторов, так и нелинейностью связи, то есть обусловлена коэффициентами  или  в выражении для потенциала (34).

Для появления четко выраженной петли в слагаемом двойной частоты в выражении (40), необходимым условием является запаздывание фазы на . Такой же сдвиг наблюдается в развертке по времени для второго осциллятора системы на рис.2б (колебания  отстают по фазе от колебаний  как раз на четверть начального периода, что хорошо видно при укрупнении масштаба).  

Таким образом, реализуемое за счет нелинейности системы возбуждение двойной частоты, объясняет общий характер колебаний в режиме №2, соответствующем умеренному уровню возбуждения системы. 

Однако при повышении уровня возбуждения, кроме второй гармоники могут образовываться третья, четвертая и более высокие, причем такое возбуждение более высокочастотных гармоник происходит постепенно без проявления каких-либо порогов.

Подобное возбуждение высших гармоник может беспороговым образом приводить к постепенному усложнению характера колебаний, то есть сначала к режиму №3, которому свойственно более дробное расщепление траекторий параметрического портрета (рис.2б), а затем к режиму №4, где гармоник возбуждается настолько много, что колебания приобретают квазистохастический характер (рис.2в).  

Дальнейшее увеличение уровня возбуждения, по достижении определенного порога, приводит к уходу системы на бесконечность (рис.2г), как это объяснено в предыдущем разделе.

    Наблюдаемый при неидентичности осцилляторов асинхронный режим №6 (рис.4) может быть обусловлен совокупным действием как умножения частоты возбуждения, так и возникновением комбинационных частот за счет различия собственных частот осцилляторов друг от друга. 

 

Заключение

Рассмотрены нелинейные вынужденные колебания намагниченности и упругого смещения в нормально намагниченной ферритовой пластине, обладающей магнитоупругими свойствами. На основе анализа полных уравнений задачи для связанных магнитного и упругого резонаторов выявлен характер связи, обусловленный магнитоупругим взаимодействием. Показано, что нелинейная связь может иметь порядок от первой до девятой степени по намагниченности.

Построена упрощенная модель системы, содержащая два связанных осциллятора, один из которых является нелинейным, а другой – линейным, причем связь между осцилляторами имеет нелинейный характер. Для такой системы показана возможность возбуждения вынужденных колебаний автомодуляционного характера, имеющих место как при идентичных параметрах обоих осцилляторов, так и при их различии.

Для случая идентичных параметров построены развертки во времени и параметрические портреты различных видов колебаний, на основе анализа которых выявлены пять основных режимов, сменяющих друг друга по мере увеличения амплитуды возбуждения: режим №1 –  регулярный синусоидальный; режим №2 – регулярный с расщеплением; режим №3 – регулярный без расщепления; режим №4 – нерегулярный квазихаотический; режим №5 – нерегулярный расходящийся. Режимы №1-№4 при увеличении амплитуды возбуждения плавно сменяют друг в друга, а режим №4 переходит в режим №5 пороговым образом. Колебания при режимах №1-3 являются периодическими, синхронными с возбуждающей силой, при режиме №4 – квазихаотическими, а при режиме №5 колебания как таковые отсутствуют и система уходит на бесконечность.  

В случае неидентичных параметров осцилляторов на основе разверток во времени и параметрических портретов выявлен двухпериодический режим асинхронных колебаний – режим №6, малый период которого соответствует периоду возбуждения, а большой в несколько раз (до порядка и более) превышает период возбуждения.   

Для интерпретации наблюдаемых явлений предложена модель обобщенного потенциала, имеющего вид суммы степенных функций, образованных произведениями обобщенных координат обоих осцилляторов вплоть до четвертого порядка. Из аналогии с магнитоупругой системой выявлена роль отдельных компонент потенциала, получен его упрощенный вид, содержащий пять слагаемых, два из которых дают собственные частоты осцилляторов, одно – нелинейность первого осциллятора и еще два слагаемых обеспечивают линейную и нелинейную связь между осцилляторами. На основе формы потенциальной поверхности проанализирована роль этих слагаемых в формировании регулярных режимов колебаний, а также выявлены условия, обеспечивающие уход системы на бесконечность.

Для объяснения сопровождающего режимы №2-№4 расщепления синусоидальных колебаний предложена модель генерации гармоник за счет нелинейности системы. Показано, что возбуждение второй гармоники приводит к регулярным автомодуляционным колебаниям, соответствующим режиму №2, а возбуждение гармоник более высоких порядков может привести к нерегулярным колебаниям вплоть до квазихаотического их характера, соответствующим режимам №3 и №4.

Высказано предположение о возможности формирования асинхронных колебаний, соответствующих режиму №6, за счет образования комбинационных частот между собственными частотами двух составляющих систему осцилляторов. 

Таким образом показано, что совокупность предложенных моделей – обобщенного потенциала и генерации гармоник или комбинационных частот, может объяснить все наблюдаемые особенности возбуждаемых автомодуляционных колебаний.

 

Благодарность

Авторы признательны к.ф.-м.н. В.С.Власову (СыктГУ) за первичную постановку задачи, помощь на предварительных этапах и постоянное стимулирующее внимание к работе.   

 

Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).

 

Литература

    1. Физическая энциклопедия. Т.1. М.: Советская энциклопедия. 1988.  Статья «Гиперзвук».

    2. Такер Дж., Рэмптон В., Гиперзвук в физике твердого тела. М.: Мир. 1975.

    3. Поверхностные акустические волны. Под ред. Олинера А. М.: Мир. 1981.

    4. Bleustein J.L. // Appl. Phys. Lett. 1968. V.13. P.412.

    5. Гуляев Ю.В. // ПЖЭТФ. 1969. Т.9. С.63. 

    6. Кикучи Е. Ультразвуковые преобразователи. М.: Мир. 1972.

    7. Ле-Кроу Р., Комсток Р. // В кн.: У. Мэзон (ред.): Физическая акустика. Т.3Б. Динамика решетки. М.: Мир. 1968. С.156. 

    8. Моносов Я.А. // Нелинейный ферромагнитный резонанс. М.: Наука. 1971.

    9. A.G. Temiryazev, M.P. Tikhomirova, P.E. Zilberman. // J. Appl. Phys. 1994. V.76. №12. P.5586. 

    10. Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ЖЭТФ. 1995. Т.108. №1. С.281.

    11. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // РЭ. 1999. Т.44. № 10. С.1262.

    12. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ФТТ. 2000 Т.42. №6. С.1062.

    13. Gerrits Th., Schneider M.L., Kos A.B., Silva T.J. // Phys.Rev.B. 2006. V.73. №9. P.094454(7).      

    14. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.

    15. Власов В.С., Шавров В.Г., Щеглов В.И. // "Журнал радиоэлектроники" [электронный журнал]. 2013. №2. c.1-34. URL: http://jre.cplire.ru/jre/feb13/10/text.html, http://jre.cplire.ru/jre/feb13/10/text.pdf.

    16. Власов В.С., Шавров В.Г., Щеглов В.И. // РЭ. 2014. Т.59. №5. С.482.

    17. Власов В.С. Исследование релаксационной и нелинейной динамики магнитных и магнитоупругих колебаний пленок и частиц. Диссертация на соискание ученой степени канд. физ.-мат. наук. МГУ. 2007.

    18. Карпачев С.Н., Власов В.С., Котов Л.Н. // Вестник МГУ. Сер.3. 2006. № 6. С.60.

    19. Власов В.С.,  Иванов А.П., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сб. тр. XX Межд. конф. «Электромагнитное поле и материалы». Москва. М.: «НИУ МЭИ». 2012. С.248.

    20. Котов Л.Н., Власов В.С., Иванов А.П., Щеглов В.И., Шавров В.Г. // Вестник Челябинского государственного университета. 2013. №25 (316). Физика. Вып.18. С.27.

    21. Weiss M.T. // Phys.Rev.Lett. 1958. V.1. №7. P.239.

    22. Weiss M.T. // Journ. Appl. Phys. 1959. Suppl. to V.30. №4. P.146S.

    23. Щеглов В.И., Шавров В.Г., Зубков В.И., Власов В.С., Котов Л.Н. // Сб. тр. XII Межд. конф. "Магнетизм, дальнее и ближнее спин-спиновое взаимодействие". Москва-Фирсановка. Изд.МЭИ. 2009. С.100.

    24. Власов В.С.,  Иванов А.П., Шавров В.Г., Щеглов В.И. //  "Журнал радиоэлектроники" [электронный журнал]. 2013. №11. http://jre.cplire.ru/jre/nov13/3/text.html, http://jre.cplire.ru/jre/nov13/3/text.pdf.

    25. Власов В.С.,  Иванов А.П., Шавров В.Г., Щеглов В.И. // "Журнал радиоэлектроники" [электронный журнал]. 2014. №1. http://jre.cplire.ru/jre/jan14/11/text.html, http://jre.cplire.ru/jre/jan14/11/text.pdf.

    26. Власов В.С.,  Иванов А.П., Шавров В.Г., Щеглов В.И. // РЭ. 2015. Т.60. №1. С.79.

    27. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // РЭ. 2015. Т.60. №3. С.297.

    28. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // Сб. тр. XXII Межд. конф. «Электромагнитное поле и материалы». Москва. М.: «НИУ МЭИ». 2014. С.161.

    29. Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука. 1973.

    30. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.

    31. Ландау Л.Д., Лифшиц Е.М.  Теория упругости (Теоретическая физика, т.VII). М.: Наука. 1965.

    32. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.

    33. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №6. С.689.

    34. Ольховский И.И. Курс теоретической механики для физиков. М.: Наука. 1970.

    35. Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. М.: ФИЗМАТЛИТ. 2003.

    36. Стрелков С.П. Введение в теорию колебаний. М.: Наука. 1964.

    37. Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М.: Наука. 1978.