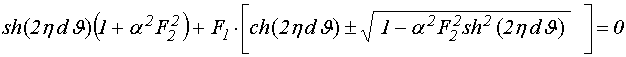"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2016

оглавление

УДК 537.874; 537.624

ПОВЕРХНОСТНЫЕ МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В ПЛАСТИНЕ ФЕРРИТА С ДИССИПАЦИЕЙ.

ЧАСТЬ 3. РАСПРОСТРАНЕНИЕ ВОЛНЫ В ПРОИЗВОЛЬНОМ НАПРАВЛЕНИИ ОТНОСИТЕЛЬНО ПОЛЯ

 

Ю. И. Келлер1, П. А. Макаров1, В. Г. Шавров2, В. И. Щеглов2

1Сыктывкарский государственный университет

2Институт радиотехники и электроники им. В.А.Котельникова РАН

 

Статья поступила в редакцию 14 февраля 2016 г.

 

Аннотация. На основе последовательного решения уравнения движения для намагниченности проведен учет затухания поверхностных магнитостатических волн (ПМСВ) в касательно намагниченной ферритовой пластине при распространении волны в произвольном направлении относительно поля. Получены законы дисперсии прямых и обратных диссипативных ПМСВ для действительной и мнимой частей комплексного волнового числа в случаях большого и малого затухания. Проведено сопоставление характера изменения дисперсии при вариациях направления распространения ПМСВ с изменением дисперсии в случае вариации затухания. Для интерпретации полученных зависимостей предложена модель сечения дисперсионной поверхности ПМСВ в пространстве трех измерений. 

Ключевые слова: феррит, магнитостатические волны, диссипация. 

Abstract. By means of consistent solution of motion equation for magnetization the  dissipation of magnetostatic surface waves (MSSW) propagating on in-plane magnetized ferrite plate in arbitrary direction relatively to field is considered. The dispersion characteristics of forward and backward dissipative MSSW for real and imaginary parts of complex wave number in the cases of large and small dissipation are found. The comparison of dispersion variation character by the changing of MSSW propagation direction with the variation of dispersion in the case of changing of dissipation is made. For the interpretation of obtained dependencies the model of cross section of MSSW dispersion surface in the space of three dimensions is proposed. 

Key words: ferrite, magnetostatic waves, dissipation.

 

Введение

Поверхностные магнитостатические волны (ПМСВ) в пленках железоиттриевого граната (ЖИГ) [1], составляют основу широкого класса устройств аналоговой обработки информации в диапазоне СВЧ [2-5]. Работы по распространению ПМСВ в пленках ЖИГ в неоднородных полях [6-11] и сложных структурах [12-17] ограничиваются случаем бездиссипативной среды. Однако в работах [18-19] показано, что диссипация кроме прямых бездиссипативных ПМСВ [1] приводит к появлению волн обратных «диссипативных». Для частного случая распространения волны перпендикулярно направлению магнитного поля, в случае учета потерь введением мнимой добавки к частоте, получены дисперсионные соотношения для действительной и мнимой частей волнового числа, выявлены некоторые особенности спектров прямых и обратных ПМСВ, в частности ограничение по волновому числу.  

В работах [20-23] показано, что распространение ПМСВ в среде с диссипацией наиболее последовательно может быть описано на основе введения комплексного волнового числа. Получены дисперсионные соотношения для действительной и мнимой частей волнового числа в случае произвольного направления распространения волны относительно магнитного поля. На основе этих дисперсионных соотношений исследованы свойства ПМСВ, распространяющихся перпендикулярно к направлению поля.

В работах [24,25] частично затронуто распространение ПМСВ в диссипативной среде в произвольном направлении относительно поля, опять путем введения мнимой добавки к частоте. Построены индикатрисы (изочастотные кривые) прямых ПМСВ и исследовано направление групповой скорости волны при изменении ориентации ее волнового вектора, однако ограничение по волновому числу не отмечено и дисперсионное соотношение в явном виде не приведено и в достаточной мере не исследовано. 

Настоящая работа является продолжением работ [22] и [23] (их третьей частью), так что, основываясь на полученных там дисперсионных соотношениях, значительно более подробно, чем в [24,25], рассматривает распространение ПМСВ в произвольном направлении относительно поля. Основное внимание будет уделено особенностям распространения ПМСВ по произвольным углом к направлению поля.

 

1. Геометрия задачи

Общая геометрия задачи совпадает с принятой в работах [20-23] и представлена например на рис.1 в работе [23]. Ферритовая пластина толщины  намагничена в плоскости полем . Декартова система координат выбрана таким образом, что ее начало, точка , находится на середине толщины пластины, плоскость  параллельна плоскости пластины, а ось  ей перпендикулярна. Координаты плоскостей пластины по оси  равны . Ось  ориентирована вдоль поля . Рассматриваются ПМСВ, распространяющиеся вдоль верхней поверхности пластины при . Волновой вектор  лежит в плоскости и  составляет угол  с осью , вектор групповой скорости  лежит в той же плоскости и составляет угол  с осью .

 

2. Параметры задачи

Основные параметры задачи совпадают с принятыми в работах [20-23]. Намагниченность материала пластины составляет . Толщина пластины  равна . Постоянное поле  в плоскости пластины равнялось . Величина угла  менялась в пределах от  до (при максимальном угле отсечки на низшей частоте спектра ПМСВ равном ). Параметр затухания  менялся в пределах от  до . Время релаксации определялось по методике, описанной в работе [23, раздел №5, рис.2], и составляло порядка . Остальные значения параметров, используемые для построения кривых, указаны в подписях к рисункам и в тексте.

Замечание. Как будет видно из дальнейшего изложения, рассматриваются два уровня затухания: малое и большое. Четкого критерия, разделяющего эти уровни, не установлено, однако «малое» затухание соответствует небольшому изменению основных зависимостей (в пределах не более ), а «большое» – приближению к предельному значению затухания, при котором распространение ПМСВ еще возможно. Так малое затухание будет соответствовать , а большое  или  (в зависимости от конкретных случаев).

 

3. Волновое число и дисперсионные соотношения

В соответствии с [20-22], волновое число ПМСВ являлось комплексным:

,                                                                                             (1)

где  и  – действительные постоянные ( и ).

Ввиду важности, приведем еще раз без вывода полученные в работе [22] дисперсионные соотношения.

Дисперсионное соотношение для действительной части волнового числа имеет вид [22, формула (115)]:

 (2)                                                                           

Дисперсионное соотношение для мнимой части волнового числа имеет вид [22, формула (137)]: 

,   (3)

Вспомогательные обозначения  и  определяются формулами [22, формулы (98),(99)]:

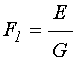;                                                                                                 (4)

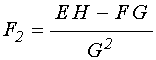,                                                                                 (5)

 

где [22, формулы (92)-(95)]:

;                                                                                      (6)

;                                                                                               (7)

;                                                         (8)

,                                                      (9)

 

в которых [22, формула (70)]:

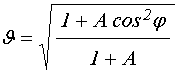,                                                                            (10)

при вспомогательных обозначениях [22, формулы (14)-(18)]:

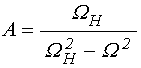;                                                                                    (11)

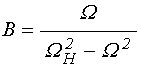;                                                                                    (12)

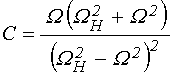;                                                                             (13)

.                                                                              (14)

 

содержащих нормированные частоты  и  в виде [22, формулы (11)-(12)]:

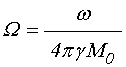;                                                                                       (15)

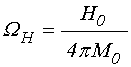.                                                                                      (16)

 

В двух последних формулах  означает частоту возбуждения,  – постоянное магнитное поле в плоскости пластины,  – намагниченность насыщения материала пластины. 

Замечание. Как пояснено в [22], эти соотношения получены в приближении малого затухания, то есть диссипативный параметр Гильберта  [26-29] полагается значительно меньшим единицы.

Характерные частотные границы областей существования прямых и обратных ПМСВ [22, формулы (23),(25),(27),(37)-(39)] при принятых значениях параметров равны:

;                                         (17)

;                                                (18)

,                     (19)

где  – гиромагнитная постоянная, равная . 

Согласно показанному в [22], прямые ПМСВ существуют в интервале частот между  и , а обратные – в интервале частот между  и , то есть  является разграничительной линией между областями прямых и обратных волн.

 

4. Основные алгоритмы расчета

В настоящей работе основные алгоритмы расчета совпадали с принятыми в [22,23]. Дисперсионные кривые, как зависимости частоты  от действительной  или мнимой  частей волнового числа, рассчитывались в соответствии с приведенными выше формулами (2) и (3) при помощи алгоритма поиска нуля.

Групповая скорость распространения волны определялась как касательная к дисперсионной кривой для действительной части волнового числа [30-32], в соответствии с формулой:

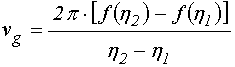,                                                                 (20)

 

где  и  – два последовательных значения волнового числа, расположенные на расстоянии одного шага.   

Групповая скорость роста затухания волны, введенная в [23], определялась по сходной формуле: 

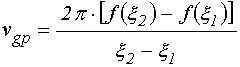,                                                                (21)

 

где  и  – два последовательных значения мнимой части волнового числа, расположенные на расстоянии одного шага.

Развитие колебаний во времени, необходимое для учета механизмов ограничения дисперсионных кривых ПМСВ, определялось по методике, описанной в работах [33-41], причем такое ограничение трактовалось в соответствии с механизмом, предложенным в работе [23, раздел №7].   

 

5. Дисперсия прямых ПМСВ при изменении действительной части волнового числа. Малое затухание

Рассмотрим сначала дисперсионные кривые прямых ПМСВ при изменении действительной части волнового числа при сравнительно малом затухании, для чего положим . Обратимся к рис.1, где представлены дисперсионные кривые прямых ПМСВ для действительной части волнового числа  при различных значения угла  между волновым вектором и направлением поля.

 

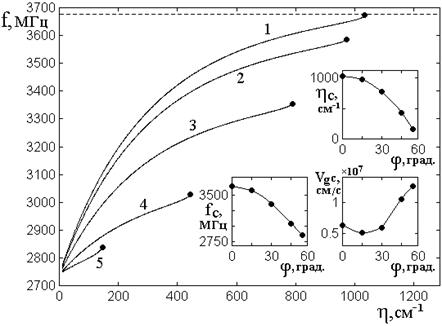
Рис.1. Дисперсионные кривые прямых ПМСВ для действительной части волнового числа при различных значениях угла .

Затухание малое: . Угол : 1 –  , 2 – , 3 – ,  4 – , 5 – .

На врезках – зависимости предельных значений ,  и  от угла .

 

Можно видеть, что по мере увеличения угла  дисперсионные кривые отклоняются вниз по частоте, а их предельная длина уменьшается. Отклонение дисперсионных кривых вниз является следствием сужения дисперсионной поверхности ПМСВ в пространстве трех измерений: , , , где эта поверхность относительно плоскости   имеет вид выгнутой кверху «полуконической крыши», сечение горизонтальной плоскостью которой сужается по мере увеличения частоты (см. напр. [42, стр.81-82, рис.4.6,4.7]. Ограничение длины дисперсионных кривых на рис.1 связано с ролью затухания и подробно рассмотрено в предыдущих частях настоящей работы [22,23]. Уменьшение такой ограниченной длины по мере увеличения  опять-таки является следствием имеющего место при этом сужения дисперсионной поверхности ПМСВ.

Интересно сопоставить этот рисунок с приведенным в работе [23] рис.3. Здесь кривая 1 построена при тех же параметрах, что и кривая 1 на рис.3 в работе [23], так что обе кривые полностью совпадают. Однако там увеличение затухания приводит к приближению кривых к вертикальной оси, тогда как здесь – тенденция обратная. С точки зрения формирования дисперсионных поверхностей, в работе [23] такая поверхность по мере увеличения затухания поднимается кверху, в результате чего линия пересечения этой поверхности с плоскостью, перпендикулярной направлению поля, также стремится кверху. В настоящей работе затухание не меняется, то есть поверхность в целом остается неизменной, тогда как частота повышается, в результате чего ветви линии пересечения поверхности с горизонтальной плоскостью сближаются, что и приводит к стремлению дисперсионных кривых на рис.1 к горизонтальной оси.    

Приведенные на врезках в рис.1 зависимости предельных значений ,  и  от угла  дополнительно характеризуют тенденции изменения этих параметров в точке обрыва дисперсионных кривых. Уменьшение предельной частоты является свойством уменьшения верхней границы спектра ПМСВ при увеличении угла  , также наглядно следующим из формы дисперсионной поверхности [42]. Так что дисперсионные кривые обрываются по волновому числу тогда, когда дисперсионная кривая достаточно близко подходит к своему верхнему пределу, соответствующему заданному значению угла . Некоторое увеличение групповой скорости вблизи точки обрыва, по-видимому, отражает ту же тенденцию сближения времени релаксации с периодом волны, что и в работе [23, раздел №7], проявляющуюся там подобным образом на врезке для в рис.3.                                                                                                                                                                                                        

Обратимся теперь к рис.2, где в тех же условиях показаны зависимости групповой скорости прямых ПМСВ от действительной части волнового числа. Кривая 1 здесь также совпадает с кривой 1 на рис.4 в работе [23], остальные кривые 2 – 5 соответствуют постепенному увеличению угла  в тех же пределах, что на рис.1.

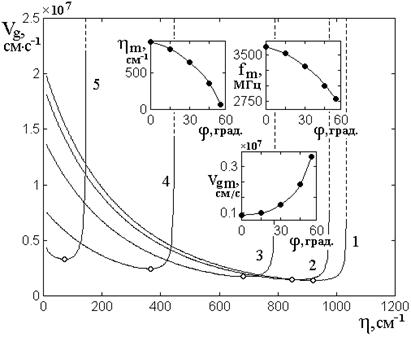
Рис.2. Зависимости групповой скорости прямых ПМСВ от действительной части волнового числа
при различных значениях угла . Все параметры – те же, что на рис.1.

На врезках – зависимости значений ,  и от угла , соответствующие минимумам основных кривых.

 

Можно видеть, что характер всех кривых – тот же, что и для кривой 1: все они по мере увеличения  сначала несколько спадают, после чего, пройдя через минимум, устремляются к плюс бесконечности. Согласно интерпретации, приведенной в работе [23, раздел №7], минимум кривых соответствует затуханию волны на расстоянии своей длины, то есть переходу к апериодическому режиму. После такого перехода происходит плавное стремление намагниченности к нулю на расстоянии, значительно превышающем длину волны, что и дает кажущееся увеличение групповой скорости, проявляющееся в росте кривых правее минимума.  

Смещение минимума в сторону меньших значений  при увеличении  обусловлен той же причиной, что и укорочение кривых на рис.1, то есть происходящим при этом уменьшением предельной частоты спектра ПМСВ.

Приведенные на врезках в рис.2 зависимости значений ,  и от угла , соответствующие минимумам основных кривых, в общем ведут себя аналогично подобным зависимостям на рис.4 в работе [23], хотя там меняется параметр затухания, а здесь – угол.

Таким образом, хотя увеличение затухания соответствует росту  крутизны дисперсионной поверхности, а увеличение угла – смещению по этой поверхности в сторону, можно заметить, что характер кривых на рис.4 в работе [23] и здесь на рис.2 качественно сходен, что связано с уменьшением по мере увеличения  максимально достижимой частоты ПМСВ в обоих этих случаях.

 

6. Дисперсия прямых ПМСВ при изменении действительной части волнового числа. Большое затухание

Рассмотрим теперь те же дисперсионные кривые прямых ПМСВ при изменении действительной части волнового числа при довольно большом параметре затухания , величина которого, согласно [23], близка к предельно допустимому значению (около ), выше которого распространение ПМСВ отсутствует. Обратимся к рис.3, где показаны те же кривые, что на рис.1, но при . Здесь кривая 1 (с точностью до масштаба по горизонтали) совпадает с кривой 4 на рис.3 в работе [23], а остальные кривые соответствуют постепенному увеличению угла .

Главным отличием от кривых, приведенных на рис.1, здесь является изменение знака выпуклости кривых: там их выпуклость направлена вверх, тогда как здесь – вниз. Однако, как можно видеть из рис.3 в [23], такое изменение знака выпуклости связано не с изменением угла , а обусловлено с увеличением затухания. Так, на том же рис.3 в [23] кривая 1, соответствующая  имеет выпуклость вверх, тогда как кривая 4 на том же рисунке, соответствующая , имеет выпуклость вниз. Поскольку кривые на рис.3 здесь только начинаются с такой кривой, то все они имеют тоже выпуклость вниз. Согласно показанному в работе [23, раздел №7], трансформация знака выпуклости с положительного на отрицательный при увеличении затухания связана с приближением времени релаксации волны к величине ее периода, приводящем в конце концов к обрыву кривых.

 

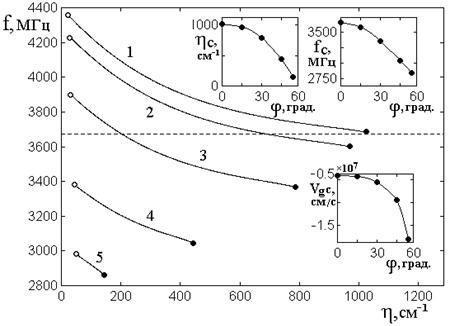
Рис.3. Дисперсионные кривые прямых ПМСВ для действительной части волнового числа при различных значениях угла .

Затухание большое: . Угол : 1 –  , 2 – , 3 – ,  4 – , 5 – .

На врезках – зависимости предельных значений ,  и  от угла .

 

По остальным свойствам, таким как ограничение по частоте и волновому числу, кривые при большом затухании (рис.3) ведут себя подобно таковым при малом (рис.1). Зависимости на врезках в рис.3 также подобны таковым на рис.1, что говорит о полном единстве механизмов, связанных с увеличением угла  , в обоих случаях как малого, так и большого затухания.

Рассмотрим теперь зависимости групповой скорости прямых ПМСВ от действительной части волнового числа при различных значениях угла   в случае большого затухания, для чего обратимся к рис.4, где представлены те же зависимости, что и на рис.2, но при .

 

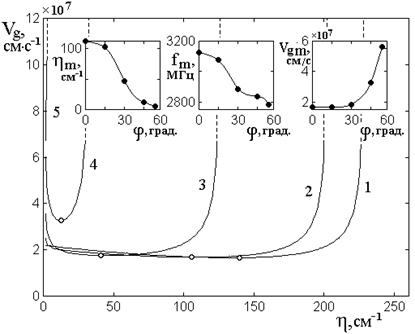
Рис.4. Зависимости групповой скорости прямых ПМСВ от действительной части волнового числа при различных значениях угла .

Параметр затухания . Все остальные параметры – те же, что на рис.2.

На врезках – зависимости значений ,  и от угла , соответствующие минимумам основных кривых.

 

Можно видеть, что приведенные здесь кривые ведут себя подобно таковым на рис.2. Интервал волновых числе соответствует таковому на рис.3. Резким отличием является значительно большая (примерно в пять раз) групповая скорость для кривых на всем их протяжении по сравнению с кривыми на рис.2. Из сравнения с рис.3 в работе [23] можно видеть, что такой рост групповой скорости обусловлен именно увеличением затухания: так кривые 2, 3, 4 на рис.3 в работе [23] идут тем круче, чем затухание больше.

В остальном поведение кривых на рис.4, в том числе на врезках, подобно таковому на рис.2 с учетом изменения масштаба по горизонтальной оси, причина чего отмечена выше.

 

7. Дисперсия обратных ПМСВ при изменении действительной части волнового числа. Малое затухание

Рассмотрим теперь дисперсионные кривые обратных диссипативных ПМСВ при изменении действительной части волнового числа. Сначала обратимся к случаю малого затухания, то есть положим . Рассмотрим рис.5, где представлены дисперсионные кривые обратных ПМСВ для действительной части волнового числа  при различных значения угла  между волновым вектором и направлением поля.

 

Рис.5. Дисперсионные кривые обратных ПМСВ для действительной части волнового числа при различных значениях угла .

Затухание малое: . Угол : 1 –  , 2 – , 3 – ,  4 – , 5 – .

На врезках – зависимости предельных значений ,  и  от угла .

 

На этом рисунке кривая 1 совпадает с кривой 1 на рис.5 в работе [23], как построенная при тех же параметрах, тогда как остальные кривые, соответствующие увеличению угла , смещаются вниз как по частоте, так и по волновому числу, причем их полная длина уменьшается.

Можно видеть, что ограничение дисперсионных кривых по волновому числу имеет место как сверху, так и снизу. Ограничение сверху (сплошные точки на концах кривых) связано с ролью затухания и подробно рассмотрено в предыдущих частях настоящей работы [22,23]. Ограничение снизу (открытые точки) выражено значительно слабее, чем сверху и связано со снижением верхней частотной границы области существования обратных ПМСВ, как это видно из рис.7 в работе [23]. Следует отметить, что на ограничении снизу увеличение угла , сказывается значительно слабее, чем увеличение затухания, как это можно видеть из сравнения с рис.5 в работе [23]. Там увеличение затухания в почти полном интервале допустимых значений параметра  (от  до ) приводит к изменению нижней границы кривых по волновому числу с  до , тогда как здесь при изменении угла  от нуля до  (то есть почти в полном интервале отсечки, соответствующем на низшей частоте спектра ), нижняя граница дисперсионных кривых увеличивается с  до всего . Следует полагать, что наблюдаемое уменьшение полной длины дисперсионных кривых по мере увеличения   обусловлено сужением дисперсионной поверхности обратных ПМСВ.

Приведенные на врезках зависимости предельных значений ,  и  при увеличении угла  имеют те же тенденции изменения, что и при увеличении затухания, иллюстрируемые врезками в рис.5 в работе [23]. Однако здесь по мере увеличения  изменение этих зависимостей ускоряется, тогда как там при увеличении затухания, по крайней мере для  и  – замедляется. Можно полагать, что такое различие обусловлено тем фактом, что увеличение затухании приводит к увеличению крутизны дисперсионной поверхности, тогда как увеличение угла   сводится только к изменению сечения поверхности, общего ее вида не меняя.

Замечание. Представленный на рис.5 ход дисперсионных кривых для обратных волн, так же как и для прямых, отражает характер сечения дисперсионной поверхности в пространстве трех измерений , , , вертикальной плоскостью, соответствующей заданному углу , однако вид этой поверхности здесь более сложен и в известной авторам литературе до настоящего времени не был исследован, поэтому авторы предполагают посвятить анализу такой поверхности отдельную  работу.  

Обратимся теперь к рис.6, где в тех же условиях показаны зависимости групповой скорости обратных ПМСВ от действительной части волнового числа. Кривая 1 здесь также совпадает с кривой 1 на рис.6 в работе [23], остальные кривые 2 – 5 соответствуют постепенному увеличению угла  в тех же пределах, что на рис.5.

 

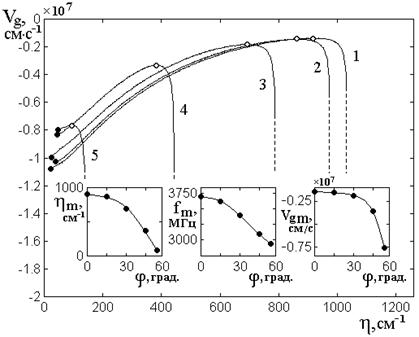
Рис.6. Зависимости групповой скорости обратных ПМСВ от действительной части волнового числа
при различных значениях угла . Все параметры – те же, что на рис.5.

На врезках – зависимости значений ,  и от угла , соответствующие максимумам основных кривых.

 

Можно видеть, что характер всех кривых – тот же, что и для кривой 1: все они по мере увеличения  сначала возрастают, после чего, пройдя через максимум, устремляются к минус бесконечности. Как и в работе [23] общий характер кривых здесь представляет собой как бы «отражение» в горизонтальной оси подобных кривых для прямых ПМСВ, приведенных на рис.2. Интерпретация их хода также аналогична.

Приведенные на врезках зависимости значений  и  от угла , соответствующие максимумам основных кривых, в общем ведут себя аналогично подобным зависимостям на рис.6 в работе [23], однако ход зависимости для  – обратный то есть частота максимума при увеличении  увеличивается от случая зависимости от , где частота максимума уменьшается. Такое различие, по-видимому, связано с тем обстоятельством, что увеличение затухания приводит к увеличению крутизны дисперсионной поверхности, тогда как увеличение угла такой поверхности не меняет.

 

8. Дисперсия обратных ПМСВ при изменении действительной части волнового числа. Большое затухание

Рассмотрим теперь характер дисперсионных кривых обратных диссипативных ПМСВ при большом уровне затухания, то есть положим . Заметим, что это значение затухания является близким к предельному для обратных волн, как это можно видеть из рис.7 в работе [23], то есть с точки зрения области существования ПМСВ такое затухание можно считать большим. Соответствующие зависимости для различных значений угла  показаны на рис.7. Кривая 1 здесь совпадает с кривой 3 на рис.5 в работе [23], как соответствующие одинаковому уровню затухания.

 

Рис.7. Дисперсионные кривые обратных ПМСВ для действительной части волнового числа при различных значениях угла .

Затухание большое: . Угол : 1 –  , 2 – , 3 – .

На врезках – зависимости предельных значений ,  и  от угла .

 

Можно видеть, что здесь, по сравнению со случаем малого затухания, представленным на рис.5, допустимый интервал изменения угла  значительно сужен. Контрольная проверка показывает, что он ограничен сверху величиной . Общий ход кривых – примерно тот же, что на рис.5, но здесь они заключены в значительно более узком интервале как по частоте, так и по волновому числу. Так на рис.5 этот интервал по частоте составляет от  до , тогда как здесь он простирается от  до , то есть сужается со  до  то есть более чем вдвое. По волновому числу такие же цифры на рис.5 составляют  и  , а на рис.7 –  и  , так что интервал сужается с  до , то есть в два с половиной раза. При этом однако по частоте интервал между кривыми, соответствующими соседним значениям угла  примерно сохраняется. Так на рис.5 интервал между серединами кривых 2 и 3 составляет около  (от  до ), а на рис.7 интервал между такими же кривыми примерно равен  (от  до ). Следствием такой близости величины интервалов при разных уровнях затухания является значительное сужение области допустимых значений угла : с  при малом затухании до  при большом, в результате чего при шаге в  на рис.7 умещается пять кривых, тогда как на рис.7 – всего три.

Приведенные на врезках зависимости предельных значений ,  и  от угла , отмеченных по концам кривых со стороны больших значений , имеют тот же характер, что и на рис.5, отражая однако сужение интервала существования ПМСВ, наблюдаемое для основных дисперсионных кривых.

Обратимся теперь к рис.8, где в тех же условиях показаны зависимости групповой скорости обратных ПМСВ от действительной части волнового числа. Кривая 1 здесь совпадает с кривой 3 на рис.6 в работе [23], остальные кривые 2 и 3  соответствуют увеличению угла  в тех же пределах, что на рис.7.

Можно видеть, что характер зависимостей совпадает с таковым для кривых, приведенных на рис.6 с тем различием, что здесь интервал кривых по волновому числу сужен в той же степени, что и на рис.7, тогда как абсолютные величины групповых скоростей заметно увеличены. Так на рис.6 максимумы кривых группируются вокруг , тогда как здесь подобным максимумам соответствуют скорости от  до . Можно полагать, то такое увеличение связано с более крутым характером дисперсионной поверхности, соответствующей рис.8, обусловленным большей величиной параметра затухания. 

 

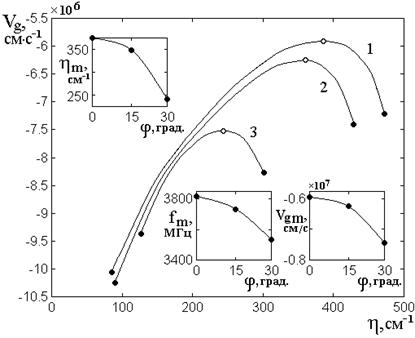
Рис.8. Зависимости групповой скорости обратных ПМСВ от действительной части волнового числа
при различных значениях угла . Все параметры – те же, что на рис.7.

На врезках – зависимости значений ,  и от угла , соответствующие максимумам основных кривых.

 

Зависимости на врезках аналогичны подобным на рис.6 с учетом сужения интервалов существования ПМСВ, отмеченного при рассмотрении рис.7.  

 

9. Дисперсия ПМСВ при изменении мнимой  части волнового числа. Малое затухание

Рассмотрим теперь роль направления волнового вектора ПМСВ в формировании дисперсии мнимой части волнового числа, для чего обратимся к рис.9. На этом рисунке показаны дисперсионные кривые ПМСВ для мнимой части волнового числа при различных значениях угла  в случае малого затухания: . Кривая 1 соответствует кривой 1 на рис.8 в работе [23], как построенная при тех же значениях всех параметров.

Замечание. Кривые на рис.9-12 построены путем полного решения уравнения (3) без каких-либо ограничений, заключенных в самом этом уравнении. Следует заметить, что в общем случае области существования как прямых, так и обратных ПМСВ по частоте имеют ограничения как сверху, так и снизу, зависимость которых от параметра затухания иллюстрируется рис.7 в работе [23]. В настоящем рассмотрении, как можно видеть из рис.1,3,5,7,  подобные ограничения также имеют место, однако на данном этапе ограничимся общим случаем полного решения уравнения (3), без их подробного учета. 

 

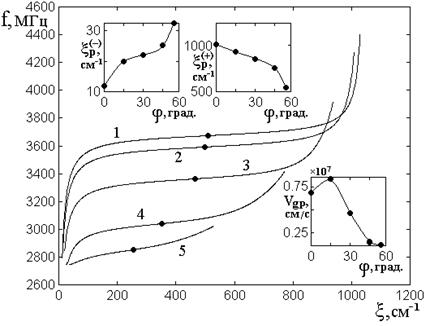
Рис.9. Дисперсионные кривые ПМСВ для мнимой части волнового числа при различных значениях угла .

Затухание малое: . Угол : 1 –  , 2 – , 3 – ,  4 – , 5 – .

На врезках показаны зависимости предельных значений  и  в точке перегиба от угла .

 

Из рис.9 можно видеть, что по мере увеличения частоты мнимая часть волнового числа всегда монотонно возрастает, то есть затухание волн при этом увеличивается. Вблизи среднего участка кривые имеют перегиб, соответствующий резкому росту затухания при переходе от прямых волн к обратным.

По мере увеличения угла  ход кривых в точке перегиба становится более крутым, то есть перегиб становится более плавным. Такое сглаживание перегиба проявляется тем сильнее, чем угол   больше.

Все кривые начинаются вблизи нижней границы существования прямых ПМСВ . Концы кривых приходятся на верхние границы существования обратных (диссипативных) ПМСВ, соответствующих заданному углу  . Так для кривой 1, где , эта частота близка к , а для других – соответственно тем ниже, чем угол  больше. Частота перегиба может быть определена как соответствующая верхней границе существования прямых ПМСВ и для кривой 1 равна .

Из рис.8 работы [23] можно видеть, что там точки перегиба для всех кривых совпадают и соответствуют  и , то есть кривые по мере увеличения затухания как бы поворачиваются вокруг этой точки в направлении против часовой стрелки. Здесь же по мере увеличения угла  кривые практически без поворота смещаются по частоте и волновому числу к меньшим значениям, при этом полная длина кривых соответственно уменьшается. Можно полагать, что подобная трансформация кривых отражает характер конфигурации сечения дисперсионной поверхности для мнимой части волнового числа, которая здесь для прямых о обратных волн является единой.

На первых двух врезках показаны зависимости предельных значений мнимой части волнового числа  и  от угла . Такой их ход отражает сужение области существования ПМСВ по мере увеличения . На третьей врезке показана зависимость групповой скорости роста затухания ПМСВ в точке перегиба от угла . Можно видеть, что несмотря на визуально кажущуюся из вида кривых 1-5 неизменность этой скорости, она после небольшого увеличения при  претерпевает некоторое уменьшение, при  достигающее почти трех раз.

Обратимся теперь к рис.10, где показаны зависимости групповой скорости роста затухания ПМСВ от мнимой части волнового числа при  и различных значениях угла . Кривая 1 здесь совпадает с кривой 1 на рис.9 в работе [23], как построенная при тех же параметрах. Остальные кривые соответствуют увеличению угла   во всей области существования ПМСВ.

 

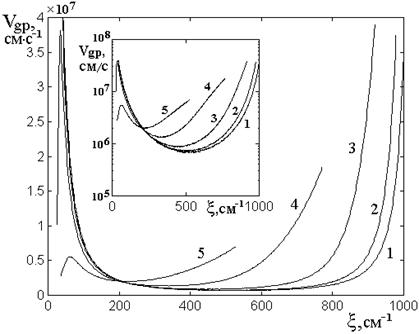
Рис.10. Зависимости групповой скорости затухания ПМСВ от мнимой части волнового числа при различных значениях угла .
Все параметры – те же, что на рис.9. На врезке показаны те же кривые в логарифмическом масштабе.

 

Можно видеть, что все кривые по мере приближения к краям области существования ПМСВ возрастают тем более резко, чем угол  меньше. Минимумы кривых приходятся на точки перегиба соответствующих зависимостей на рис.9. Рост взаимно противоположных ветвей кривых заканчивается при тех значениях , при которых кривые на рис.9 выходят на верхний и нижний пределы по частоте.

Отличие от кривых, соответствующих росту затухания (рис.9 в работе [23]), состоит в том, что там все кривые были как бы симметрично вложены друг в друга, что было вызвано совпадением точек перегиба, тогда как здесь по мере увеличения угла  кривые как целое смещаются в сторону меньших значений , что соответствует аналогичному смещению точек перегиба кривых на рис.9.

Можно отметить участок аномального максимума зависимостей  от , имеющий место для кривых 4 и 5 в окрестности . Наличие такого участка говорит об аномальной деформации дисперсионной поверхности вблизи малых значений волновых чисел.

На врезке показаны те же зависимости в логарифмическом масштабе, несколько более наглядно иллюстрирующие ход кривых  в области минимумов.

 

10. Дисперсия ПМСВ при изменении мнимой  части волнового числа. Большое затухание

Рассмотрим теперь роль направления волнового вектора ПМСВ в формировании дисперсии мнимой части волнового числа в случае большого затухания, для чего обратимся к рис.11, где показаны дисперсионные кривые ПМСВ для мнимой части волнового числа при различных значениях угла  в случае большого затухания: . Здесь кривая 1 с точностью до масштаба по осям совпадает с кривой 4 на рис.8 в работе [23], как построенная при тех же значениях параметров.

Можно видеть, что здесь кривые по мере увеличения угла  проявляют те же тенденции, что и на рис.9, с тем однако отличием, что здесь, в соответствии с увеличением затухания, крутизна всех кривых значительно возрастает, в результате чего по значению волнового числа они располагаются заметно теснее. Кривые 1-4 имеют более или менее заметно выраженный перегиб, тогда как на кривой 5, соответствующей максимально допустимому значению угла , перегиб уже отсутствует. Показанные на врезках зависимости  и  от угла . подобны таковым, приведенным на рис.9, отличаясь лишь более узкими диапазонами изменения параметров.

 

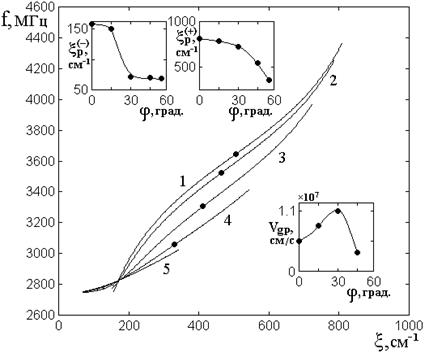
Рис.11. Дисперсионные кривые ПМСВ для мнимой части волнового числа при различных значениях угла  
 случае большого затухания: . Угол : 1 –  , 2 – , 3 – ,  4 – , 5 – .

На врезках показаны зависимости предельных значений  и  в точке перегиба от угла .

 

Обратимся теперь к рис.12, где показаны зависимости групповой скорости роста затухания ПМСВ от мнимой части волнового числа при различных значениях угла  и большом затухании . Кривая 1 здесь с точностью до масштаба совпадает с кривой 4 на рис.9 в работе [23], как построенная при тех же параметрах. Остальные кривые соответствуют увеличению угла   во всей области существования ПМСВ.

 

Рис.12. Зависимости групповой скорости затухания ПМСВ от мнимой части волнового числа при различных значениях угла
в случае большого затухания: . Все параметры – те же, что на рис.11.

 

Можно видеть, что здесь общий характер кривых подобен таковому на рис.10, однако здесь кривые в области малых волновых чисел при тех же углах  отличаются значительно большим относительным разнесением по значениям , что отражает  большее влияние затухания.

Аномальный максимум впервые проявляется на кривой 2, соответствующей , причем по мере увеличения   до  (кривая 4) переходит в перегиб, после чего на его месте при  появляется полого возрастающий участок (кривая 5), отражающий отсутствие точки перегиба на кривой 5 на рис.11. Такой ход кривых дополнительно свидетельствует в пользу сложного характера дисперсионных поверхностей при малых значениях мнимой части волнового числа.  

 

Заключение

В геометрии плоскопараллельной намагниченной в плоскости ферритовой пластины с использованием дисперсионных соотношений для компонент комплексного волнового числа в диссипативной среде, исследована дисперсия прямых и обратных ПМСВ при распространении волны в произвольном направлении относительно поля.

Приведены алгоритмы численного  расчета дисперсионных зависимостей для действительной и мнимой частей волнового числа, а также групповых скоростей распространения и роста затухания волны.

Построены дисперсионные кривые прямых ПМСВ при изменении действительной части волнового числа в случае малого затухания. Показано, что по мере увеличения угла между волновым вектором ПМСВ и направлением поля, дисперсионные кривые отклоняются вниз по частоте, а их предельная длина уменьшается.

Полученные результаты интерпретированы на основе представления о сечении плоскостью дисперсионной поверхности ПМСВ в пространстве трех измерений: частоты и двух координатных компонент действительной части волнового числа.

Проведено сравнение с характером дисперсионных кривых при изменении затухания. Показано, что различный вид дисперсионных зависимостей, соответствующих изменению затухания и направления распространения, обусловлен тем фактом, что рост затухания приводит к увеличению крутизны дисперсионной поверхности, тогда как отклонение волнового вектора волны от нормали к направлению поля вида дисперсионной поверхности не меняет, а лишь приводит к повороту секущей плоскости вокруг нормали к поверхности магнитной пластины.  

Те же дисперсионные кривые прямых ПМСВ при изменении действительной части волнового числа проанализированы в случае большого затухания. Выявлено, что отличие от случая малого затухания состоит в отклонении дисперсионных кривых по мере увеличения угла не вниз, а вверх по частоте. Показано, что такое различие обусловлено общей тенденцией отклонения дисперсионных кривых при увеличении затухания по частоте вверх, причина которого состоит в приближении времени установления стационарной амплитуды волны к ее временному периоду и связанным с этим переходом к апериодическому режиму.

Рассмотрены зависимости групповой скорости прямых ПМСВ от действительной части волнового числа в условиях малого и большого затухания. Показано, что при малых значениях волнового числа групповая скорость уменьшается, после чего, пройдя через минимум, при достаточно больших волновых числах увеличивается, стремясь к бесконечности. Выявлено, что причиной минимума является затухание волны на расстоянии своей длины, то есть переход к апериодическому режиму, после чего происходит плавное стремление намагниченности к нулю на расстоянии, значительно превышающем длину волны, что и дает кажущееся увеличение групповой скорости.

Построены дисперсионные кривые обратных диссипативных ПМСВ при изменении действительной части волнового числа в случае малого и большого затухания. Показано, что по мере увеличения угла отклонения волнового вектора ПМСВ от нормали к направлению поля дисперсионные кривые для обратных волн смещаются вниз как по частоте, так и по волновому числу, причем их полная длина уменьшается, так что ограничение дисперсионных кривых по волновому числу происходит как сверху, так и снизу, что отражает сложный характер соответствующей дисперсионной поверхности. 

Рассмотрены зависимости групповой скорости обратных ПМСВ от действительной части волнового числа в условиях малого и большого затухания. Показано, что соответствующие кривые при малых значениях волнового числа сначала возрастают, после чего, пройдя через максимум, при достаточно больших волновых числах спадают, стремясь к бесконечности, то есть являются как бы «зеркальным отражением» в горизонтальной оси подобных кривых для прямых ПМСВ, причем интерпретация хода кривых является той же самой.  

Различие между случаями малого и большого затухания состоит в том, что при большом затухании интервал допустимых отклонений волнового вектора волны от нормали к направлению поля значительно сужается, однако интервал по частоте между зависимостями, соответствующими равноотстоящим друг от друга значениям угла сохраняется, что приводит к усилению ограничения кривых как по частоте, так и по волновому числу. 

Построены дисперсионные кривые прямых и обратных ПМСВ при изменении мнимой части волнового числа в случае малого и большого затухания. Показано, что по мере увеличения частоты мнимая часть волнового числа всегда монотонно возрастает, то есть затухание волн при этом увеличивается. Вблизи среднего участка кривые имеют перегиб, соответствующий резкому росту затухания при переходе от прямых волн к обратным. По мере увеличения угла между волновым вектором и направлением поля кривые практически без поворота смещаются по частоте и волновому числу к меньшим значениям, при этом полная длина кривых соответственно уменьшается.

Исследованы зависимости групповой скорости роста затухания ПМСВ от мнимой части волнового числа при малом и большом затухании. Показано, что все кривые, имея вблизи середины области существования ПМСВ минимум, по мере приближения к ее краям возрастают тем более резко, чем угол между волновым вектором и направлением поля меньше, причем положение минимума по мере увеличения этого угла смещается в сторону меньших значений мнимой части волнового числа.

Различие между случаями малого и большого затухания состоит в том, что при большом затухании крутизна дисперсионных кривых в точке перегиба увеличивается тем сильнее, чем затухание больше, причем интервал существования ПМСВ по волновому числу и частоте сужается. Рост зависимостей групповой скорости в области малых значений мнимой части волнового числа сменяется спадом, отделенным от области роста локальным максимумом, величина которого по мере увеличения угла спадает вплоть до полного исчезновения.

 

Благодарность

Авторы признательны сотрудникам ИРЭ РАН (Фрязинской части): д.ф.-м.н. В.И.Зубкову, д.ф.-м.н. Э.Г.Локку и д.ф.-м.н. А.В.Вашковскому за консультации на начальном этапе работы, а также д.ф.-м.н. С.В. Герусу и к.ф.-м.н. А.Ю.Анненкову за ознакомление с материалами работ  [24,25]. Отдельная благодарность к.ф.-м.н. В.С.Власову (СыктГУ) за внимание к работе и многочисленные стимулирующие замечания.

 

Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).

 

Литература

1. Damon R.W., Eshbach J.R. // J. Phys. Chem. Solids. 1961. V.19 №3/4. P.308.

2. Адам Дж.Д. // ТИИЭР. 1988. Т.76. №2. С.73.

3. Исхак В.С. // ТИИЭР. 1988. Т.76. №2. С.86.

4. Шлеман Э.Ф. // ТИИЭР. 1988. Т.76. №2. С.105.

5. Adam J., Davis L., Dionne G., Schloemann E., Stitzer S. // IEEE Trans. on MTT. 2002. V.50. №3. P.721.

6. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ПЖТФ. 1989. Т.15. №4. С.1.

7. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ПЖТФ. 1989. Т.15. №4. С.5.

8. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ЖТФ. 1990. Т.60. №7. С.138.

9. Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1990. Т.35. №8. С.1617.

10. Vashkovsky A.V., Lock E.H., Shcheglov V.I., Zubkov V.I. // IEEE Trans. on Magn. 1990. V. Mag-26. №5. P.1480.

11. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1991. Т.36. №1. С.18.

12. Зубков В.И., Щеглов В.И. // РЭ. 2000. Т.45. №4. С.471.

13. Зубков В.И., Щеглов В.И. // РЭ. 2001. Т.46. №4. С.433.

14. Зубков В.И., Щеглов В.И. // РЭ. 2006. Т.51. №3. С.328.

15. Зубков В.И., Щеглов В.И. // РЭ. 2007. Т.52. №6. С.701.

16. Зубков В.И., Щеглов В.И. // РЭ. 2009. Т.54. №9. С.1064.

17. Зубков В.И., Щеглов В.И. // РЭ. 2012. Т.57. №5. С.565.

18. Вызулин С.А., Розенсон А.Э., Шех С.А. // РЭ. 1991. Т.36. №1. С.164-168.

19. Вызулин С.А. Обобщенные плоские волны в задачах электродинамики магнитогиротропных сред. Диссертация. на соискание уч. ст. д.ф.-м.н. Краснодар. 2000.

20. Макаров П.А., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2014. №7. С.1-31. http://jre.cplire.ru/jre/jul14/8/text.html,

http://jre.cplire.ru/jre/jul14/8/text.pdf.

21. Макаров П.А., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.221-236.

22. Келлер Ю.И., Макаров П.А., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2016. №2. URL:  http://jre.cplire.ru/jre/feb16/2/text.html; http://jre.cplire.ru/jre/feb16/2/text.pdf.

23. Келлер Ю.И., Макаров П.А., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2016. №3. URL: http://jre.cplire.ru/jre/mar16/1/text.html, http://jre.cplire.ru/jre/mar16/1/text.pdf

24. Annenkov A.Yu., Gerus S.V. // Book of Abstracts of Moscow International Symposium on Magnetism (MISM). 2014. Published by “Изд-во Физ.фак. МГУ". Moscow. P.863.

25. Анненков А.Ю., Герус С.В. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.99-102.

26. Гуревич А.Г. Ферриты на сверхвысоких частотах. М.: Гос.Изд.физ.-мат.лит. 1960. 

27. Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука. 1973.

28. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.

29. Gilbert T.L. // IEEE Trans. on Magn. 2004. V.40. №6. P.3443.

30. Ландсберг Г.С. Оптика. М.: Наука. 1976.

31. Вайнштейн Л.А. Групповая скорость затухающих волн. // ЖТФ. 1957. Т.27. №11. С.2606.

32. Гинзбург В.Л. Распространение электромагнитных волн в плазме. М.: Наука. 1967.

33. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.

34. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №6. С.689.

35. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №1. С.84.

36. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №6. С.719.

37. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №9. С.1120.

38. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №5. С.501.

39. Власов В.С., Кирушев М.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №8. С.806.

40. Власов В.С., Кирушев М.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №9. С.857.

41. Власов В.С., Котов Л.Н., Щеглов В.И.  Нелинейная прецессия вектора намагниченности в условиях ориентационного перехода (монография). Сыктывкар: ИПО СыктГУ. 2013.

42. Вашковский А.В., Стальмахов В.С., Шараевский Ю.П. Магнитостатические волны в электронике сверхвысоких частот. Саратов: Изд.Саратовского университета. 1993.