| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6 , 2000 |
МЕТОДЫ
ОПТИЧЕСКОЙ СОГЛАСОВАННОЙ ФИЛЬТРАЦИИ
В ТОЧНОМ ПРИБОРОСТРОЕНИИ
В. И. Шанин, О. В. Шанин
Получена 4 мая 2000 г.
Введение
1. Принцип
работы голографического коррелятора
2. Теоретический анализ
метрологических возможностей
голографического коррелятора
3. Разработка методов повышения
чувствительности голографического
коррелятора
3.1. Преобразование информации в
частотной плоскости коррелятора
3.2. Преобразование
информации в предметной плоскости.
3.3.
Разработка метода оптической фильтрации с
противофазной компенсацией для
допусковой
разбраковки деталей
4. Установление требований к
точности позиционирования деталей.
5. Ограничения
метода
6. Результаты
экспериментальных исследований
6.1. Описание
экспериментальной установки и проведения
экспериментов
6.2. Исследование
влияния преобразования информации в
частотной плоскости на
корреляционный
отклик
6.3. Разработка
метода оптической фильтрации с
противофазной компенсацией для допусковой
разбраковки деталей
6.4.
Исследование влияния преобразования
информации в предметной плоскости на
корреляционный
отклик
7. Основные
концепции построения систем контроля
Выводы
Литература
В статье рассмотрены возможности применения методов оптической согласованной фильтрации для решения задач автоматического контроля геометрических параметров деталей точного приборостроения. Здесь представлены результаты теоретических и экспериментальных исследований точностных возможностей голографического коррелятора, установлены требования к позиционированию деталей на его входе, а также показана возможность допусковой разбраковки деталей с помощью голографического фильтра, синтезированного методом двойной экспозиции с противофазной компенсацией.
Получены аналитические зависимости поведения корреляционного отклика от изменения размеров, смещения и угловой ориентации деталей. Установлено, что относительная точность контроля составляет 0,5%. Для повышения абсолютной точности контроля предложено использовать преобразование волновых полей как на входе, так и в частотной области коррелятора. Это позволило на порядок повысить точность методов оптической согласованной фильтрации. Результаты экспериментальных исследований хорошо согласуются с данными теоретического анализа.
Современная технология точного приборостроения предъявляет весьма жесткие требования к качеству и надежности комплектующих деталей, что может быть обеспечено лишь их 100% контролем.
Контроль конфигурации и линейных размеров деталей точного приборостроения осуществляется с помощью проекторов и микроскопов, разработанных еще в 70-е годы [1]. Процедура контроля здесь производится человеком, требует значительных затрат времени и поэтому мало производительна. Создание автоматических систем на базе этих средств измерения сопряжено с серьезными техническими трудностями, преодолеть которые, как правило, не удается. В этой связи изыскание и разработка иных методов и средств контроля представляется весьма актуальной задачей. Проблема усугубляется еще и тем, что приходится учитывать такие требования производства как:
- бесконтактность
операции контроля;
- соответствие скорости контроля темпу
выпуска деталей;
- обеспечение ориентации деталей на позиции
контроля существующими средствами;
- обеспечение требуемой точности контроля;
- экономическая целесообразность.
Большинству перечисленных требований удовлетворяют уже нашедшие применение в различных областях науки и техники, в том числе и при решении задач контроля [2], одно из ярких достижений радиофизики - когерентно-оптические методы обработки информации [3]. Среди них наибольшего внимания заслуживают методы оптической согласованной фильтрации с голографическим фильтром [27]. Они обладают рядом практически важных достоинств, к которым следует отнести; простоту алгоритма обработки информации; удобство сопряжения со средствами автоматики; оперативность перестройки для обработки нового вида информации; высокое быстродействие. Однако для применения оптической согласованной фильтрации в точном приборостроении, спецификой которого являются малые размеры деталей и жесткие требования к отклонению размеров от заданных, необходимо детальное исследование таких вопросов как метрологические возможности метода согласованной фильтрации, требования к ориентации детали на позиции контроля, а также возможность проведения разбраковки деталей в требуемом поле допусков и концепция построения систем контроля. Рассмотрению этих вопросов и посвящена настоящая работа.
1. Принцип работы голографического коррелятора
Типовая схема, реализующая метод оптической согласованной фильтрации на базе голографического фильтра и которая известна как голографический коррелятор, показана на рис.1. Ее принцип работы основан на сравнении входного образа с эталонным. Применительно к контролю здесь принятие решения о качестве контролируемой детали осуществляется по величине выходного сигнала коррелятора, математически описываемого выражением [4,5]
где ![]() — переменный параметр, характеризующий
состояние контролируемой детали;
— переменный параметр, характеризующий
состояние контролируемой детали; ![]() — координаты плоскости фильтрации;
— координаты плоскости фильтрации; ![]() - амплитудное пропускание входной
плоскости с эталонной деталью;
- амплитудное пропускание входной
плоскости с эталонной деталью; ![]() — амплитудное пропускание входной
плоскости с контролируемой деталью;
— амплитудное пропускание входной
плоскости с контролируемой деталью; ![]() — символ операции корреляции.
— символ операции корреляции.
Рис.1. Схема голографического коррелятора, где:
1 - лазер, 2 - коллиматор, 3 - входная плоскость, 4 и 6 - оптические системы для Фурье-преобразования, 5 - голографический фильтр, 7 - выходная плоскость.
Особенностью
рассматриваемой схемы является то, что
выходной сигнал функция взаимной
корреляции (1) вычисляется не в
предметной (входной), а в частотной
плоскости. Для этого контролируемая деталь
размещается во входной плоскости 3 и
освещается плоской волной света,
сформированной коллиматором 2 из излучения
лазера 1. Прошедший через входную плоскость
свет поступает на оптическую систему 4, в
задней фокальной плоскости которой
формируется Фурье-спектр
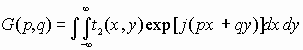 , где
, где ![]() — координаты входной плоскости;
— координаты входной плоскости; ![]() — амплитудное пропускание входной
плоскости с контролируемой деталью;
— амплитудное пропускание входной
плоскости с контролируемой деталью; 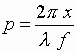 и
и 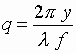 — пространственные частоты;
— пространственные частоты; ![]() — длина волны лазерного излучения;
— длина волны лазерного излучения; ![]() - фокусное расстояние оптической системы.
Здесь же находится голографический фильтр 5
с передаточной характеристикой, комплексно
сопряженной с Фурье-спектром
- фокусное расстояние оптической системы.
Здесь же находится голографический фильтр 5
с передаточной характеристикой, комплексно
сопряженной с Фурье-спектром 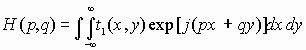 ,
где
,
где ![]() —
амплитудное пропускание входной плоскости
с эталонной деталью. На выходе фильтра
распределение света представляет
собой результат перемножения Фурье-спектра
от контролируемой детали с передаточной
характеристикой фильтра, т.е.
—
амплитудное пропускание входной плоскости
с эталонной деталью. На выходе фильтра
распределение света представляет
собой результат перемножения Фурье-спектра
от контролируемой детали с передаточной
характеристикой фильтра, т.е. ![]() ,
где
,
где ![]() —
символ операции комплексного сопряжения.
После прохождения полученного
распределения света через оптическую
систему 6, которая
выполняет обратное преобразование Фурье, в
ее частотной задней фокальной плоскости
формируется корреляционный отклик в
соответствии с выражением (1).
Корреляционный отклик имеет вид яркого
светового пятна, интенсивность которого
равна
—
символ операции комплексного сопряжения.
После прохождения полученного
распределения света через оптическую
систему 6, которая
выполняет обратное преобразование Фурье, в
ее частотной задней фокальной плоскости
формируется корреляционный отклик в
соответствии с выражением (1).
Корреляционный отклик имеет вид яркого
светового пятна, интенсивность которого
равна ![]() .
Интенсивность корреляционного пятна
с помощью фотоприемника 7
преобразуется в электрический сигнал,
который анализируется электронными средствами
и по результатам анализа принимается
решение о качестве контролируемой детали.
При принятии решения о качестве контролируемой
детали производится
оценка величины относительной
интенсивности в
корреляционном отклике, определяемой
соотношением
.
Интенсивность корреляционного пятна
с помощью фотоприемника 7
преобразуется в электрический сигнал,
который анализируется электронными средствами
и по результатам анализа принимается
решение о качестве контролируемой детали.
При принятии решения о качестве контролируемой
детали производится
оценка величины относительной
интенсивности в
корреляционном отклике, определяемой
соотношением
где
Таким образом, из алгоритма работы коррелятора следует, что для установления его метрологических возможностей и требований к ориентации деталей на позиции контроля необходимо исследовать зависимость функции взаимной корреляции (1) от упомянутых факторов.
2. Теоретический анализ метрологических возможностей голографического коррелятора
Идеальным состоянием любого производства является с одинаковыми размерами. В этом случае функция взаимной корреляции (1) переходит в автокорреляционную функцию и величина выходного сигнала коррелятора получается максимальной.
На практике в силу различных технологических причин размеры деталей одной партии, как правило, отличаются друг от друга. Поэтому приходится проводить их контроль, а в целях обеспечения достоверной разбраковки деталей разрабатываемые методы и средства контроля должны обладать необходимой точностью измерения. В приборостроении (например, часовой и авиационной промышленности) погрешность измерения линейных размеров для большинства составляет (5
-10) мкм. В этой связи представляется целесообразным установление метрологических возможностей голографического коррелятора.Для упрощения математических
выкладок анализ точности измерения
линейных размеров проведем на примере
контроля детали в виде квадратного
отверстия со стороной ![]() .
При этом отметим, что полученных
результатов от такой конкретизации
нисколько не страдает, поскольку
аналогичные данные были получены нами и при
рассмотрении деталей других конфигураций,
в частности, круглого отверстия [5],
которое является представителем широкого
класса деталей точного приборостроения,
описываемых кривыми второго порядка.
.
При этом отметим, что полученных
результатов от такой конкретизации
нисколько не страдает, поскольку
аналогичные данные были получены нами и при
рассмотрении деталей других конфигураций,
в частности, круглого отверстия [5],
которое является представителем широкого
класса деталей точного приборостроения,
описываемых кривыми второго порядка.
Амплитудное пропускание входной плоскости коррелятора с расположенной в ней контролируемой деталью можно записать в виде
где ![]() — отношение размеров сторон квадратов
контролируемой и эталонной деталей.
Пропускание же входной плоскости
коррелятора с эталонной деталью будет
описываться следующим выражением
— отношение размеров сторон квадратов
контролируемой и эталонной деталей.
Пропускание же входной плоскости
коррелятора с эталонной деталью будет
описываться следующим выражением
После подстановки (3) и (4) в (1), интегрирования и нормирования получим следующее аналитическое выражение для распределения интенсивности в корреляционном отклике
где 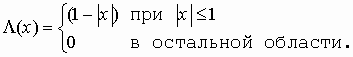
При ![]() ,
что соответствует физическим условиям
оценки корреляционного отклика, выражение (5)
принимает вид
,
что соответствует физическим условиям
оценки корреляционного отклика, выражение (5)
принимает вид
или при переходе к относительному отклонению размера детали
![]() ,
,
окончательно будем иметь
Характер
поведения зависимости (7) в
окрестности ее максимального значения, а
именно эта область
представляет интерес для оценки предельных
метрологических возможностей коррелятора,
показан на рис.2. Анализ
полученной зависимости с учетом достижимой
точности измерения интенсивности
корреляционного отклика с помощью
существующих фотоприемников (~ 2% [6])
позволяет установить, что относительная
погрешность измерения размера детали не
превышает 0,5% или ![]() .
Нетрудно убедиться, что такая точность не всегда
оказывается достаточной для
удовлетворения потребностей точного
приборостроения. Так, например,
при разбраковке деталей с погрешностью в 5
мкм полученной точности достаточно лишь
для контроля деталей,
размеры которых не
превосходят 1 мм.
.
Нетрудно убедиться, что такая точность не всегда
оказывается достаточной для
удовлетворения потребностей точного
приборостроения. Так, например,
при разбраковке деталей с погрешностью в 5
мкм полученной точности достаточно лишь
для контроля деталей,
размеры которых не
превосходят 1 мм.
Однако, проведенные нами исследования позволили установить, что голографический коррелятор можно применять и для контроля деталей больших размеров.
Рис.2. Зависимость интенсивности корреляционного отклика от изменения величины отклонения e
|
Введение, |