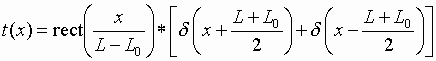При проведении анализа метрологических возможностей голографического коррелятора для задач контроля линейных размеров деталей в разделе 3 предполагалось, что положения контролируемой и эталонной деталей на входе коррелятора совпадают. В реальных же условиях производства за счет дестабилизирующих факторов следует ожидать рассогласования между их положениями. Поэтому представляет практический интерес исследование поведения максимума корреляционного отклика от ориентации детали на входе коррелятора. Под ориентацией понимается:

- положение контролируемой детали относительно центра апертуры иди маски относительно центра контролируемой детали;

- рассогласование между угловыми положениями контролируемой и эталонной деталями.

Анализ влияния каждого из видов ориентации на максимум корреляционного отклика будем проводить в предположении, что по другому виду ориентации положения деталей совпадают.

Для установления требований к точности расположения детали внутри входной апертуры необходимо в общем случае знать влияние ориентации на максимум корреляционного отклика по двум координатам. Однако при подаче детали на позицию контроля с непрерывным перемещением детали через нее достаточно найти влияние лишь по одной координате, поскольку совмещение по другой координате обеспечивается автоматически. С математической точки зрения это означает, что достаточно провести анализ поведения корреляционного отклика при контроле одномерной детали типа щель.

Пропускание щели, когда оси маски и щели совпадают, можно записать в виде

,                                              (26)

где — ширина щели; — ширина маски, — символ операции свертки и — обобщенная функция Дирака.

Амплитудное пропускание входной плоскости коррелятора при параллельном сдвиге щели относительно маски запишется как

,                                                     (27)

где — смещение маски относительно щели.

После подстановки (26) и (27) в (1), интегрирования и нормирования получим аналитическое выражение для центрального пика корреляционного отклика

                                               (28)

Положив , что как уже отмечалось, соответствует физическим условиям работы системы контроля, окончательно будем иметь

.                                                                                           (29)

График зависимости (29) показан на рис.10. Видно, что с учетом доверительного интервала измерений существующих фотоприемников точность расположения детали относительно оси маски должна быть на хуже 0,02 размера пропускающей свет области. Несложный расчет показывает, что такая точность ориентации деталей на позиции контроля обеспечивается существующими техническими средствами.

Из теории голографической обработки информации известно [38], что на величине корреляционного отклика сказывается влияние угловой ориентации анализируемого и эталонного образов. Причем величина уменьшения отклика для различных по конфигурации образов будет личной.

Поскольку основную массу деталей в точной приборостроении составляют детали с конфигурацией, описываемой кривыми второго порядка, то ограничимся рассмотрением случая контроля детали с конфигурацией в виде эллипса.

Амплитудное пропускание входной плоскости коррелятора от такой детали будет иметь вид

                                                              (30)

где и — большая и малая оси эллипса соответственно.

После подстановки (30) в (1), интегрирования и нормирования получим следующее выражение для максимума корреляционного отклика для малых (в пределах нескольких градусов) угловых отклонений контролируемой детали от эталонного положения

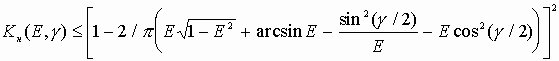,                 (31)

где — угол поворота детали относительно эталонного положения, . На рис.11 представлены зависимости выражения (31) от изменения угла для трех значений отношения .

Из сравнения кривых видно, что уменьшение максимума корреляционного отклика на (1¸2)% соответствует угловому отклонению контролируемой детали от эталонного положения на (0,5¸1)° . Технически такая точность ориентации вполне обеспечивается существующими средствами.

В голографических системах обработки информации фотоприемник обычно представляет собой комбинацию отверстия, располагаемого по центру автокорреляционного отклика, и фотоумножителя. При этом требуется точное положение фотоумножителя в выходной плоскости системы контроля. Отметим, что такая схема считывания корреляционного сигнала позволяет обрабатывать лишь часть информации, содержащейся в ней, и фотоприемник должен выбираться с учетом структуры корреляционного сигнала. Теперь, принимая во внимание то, что фототок схемы считывания линейно зависит от интенсивности корреляционного отклика, поступающей на отверстие, получим

.                                                                                   (32)

Поскольку разложение в ряд выражения (13) описывает интенсивность корреляционного сигнала в точке , то предыдущие рассуждения в отношении вопроса оптимизации являются правомочными в том случае, если использован точечный фотоприемник, расположенный в точке . Из анализа выражений (9) и (10) следует, что допустимый радиус отверстия может быть равен

.                                                                                              (33)

Здесь фазовым членом можно пренебречь.

Техническая реализация метода согласованной фильтрации базируется на двух ограничениях. Они относятся к выборке информации и влиянию положения и ориентации контролируемого изделия на входе системы контроля на корреляционный отклик.

О выборке информации говорят тогда, когда контролируются несколько дефектов среди множества дефектов, которые имеют большой допуск. При этом фильтр можно оптимизировать, если все остальные дефекты рассматриваются как детерминированный шум. Короче, метод оказывается не эффективным в том случае, когда требуется устранить влияние на кривую отклика всех дефектов, контролировать которые не надо. Поэтому приходится использовать соответствующие маски, чтобы выделить требуемые дефекты. Маскирование пространственного спектра является эффективным по той причине, что оно позволяет отделить спектральную область, наиболее чувствительную к исследуемому дефекту.

Даже в том случае, когда нет необходимости выделения конкретной информации, измерение корреляционного пика представляется весьма полезной операцией, так как она дает возможность качественно оценить подобие между сравниваемыми деталями. Поскольку в измеренном сигнале суммируются все возможные дефекты, то такой сигнал труден для количественной оценки допусков.

Влияние положения и ориентации детали на входе системы контроля на ее корреляционный отклик показано в разделе 4. В пределах поля допусков позиционирования, достижимых с помощью существующих механических средств, оптическая система может рассматриваться как пространственно инвариантная система обработки информации. Поэтому параллельный перенос детали на входе системы будет сказываться лишь на положении корреляционного пика и не будет сказываться на величине его амплитуды.

Для обнаружения малых изменений формы детали необходимо измерять распределение энергии в вершине корреляционного пика. Площадь, под которой можно интегрировать энергию, должна быть меньше размера, разрешаемого фотоприемником. Поэтому влияние положения детали на корреляционный отклик будет зависеть от метода, используемого для измерения корреляционного пика.

Здесь наиболее пристального внимания заслуживают три метода и измерения корреляционного сигнала.

1. Корреляционная плоскость регистрируется фотографически и затем исследуется фотометрическими методами. Этот метод обладает высокой точностью измерения, но труден в реализации работы системы контроля в реальном масштабе времени.

2. Корреляционная плоскость анализируется с помощью видикона, решетки фотодиодов или других подобных приборов. Такие приборы, как правило, имеют типичную неравномерность выходного сигнала порядка 10%, тем самым ограничивая их применение в случаях, когда точностные требования не очень высокие (обычно точность линейных размеров детали от 5 до 10% с ошибкой в 1 или 2%).