УДК 621.317.08; 621.317.1; 621.317.6
ПРЕДСТАВЛЕНИЕ МОДЕЛЕЙ СИГНАЛОВ В СИСТЕМЕ ИДЕНТИФИКАЦИОННЫХ ПАРАМЕТРОВ
А. А. Горшенков, Ю. Н. Кликушин
Омский государственный технический университет (ОмГТУ)
Получена 7 сентября 2010 г.
Аннотация. Предлагается новая форма записи
моделей сигналов, обобщающая классические представления. Рассмотрена структурная
схема определения идентификационных параметров, являющихся числовыми
коэффициентами модели. Даны примеры, поясняющие ряд введенных понятий.
Ключевые слова: идентификационные измерения, классификация, модель, форма и характер сигнала.
ВВЕДЕНИЕ
Начиная с 2000 года, в Журнале радиоэлектроники стали появляться публикации [1-10], отражающие развитие различных аспектов нового научного направления в теории и технике измерений - идентификационных измерений (ИИ) сигналов. Обобщение этих публикаций представлено, в частности, в монографиях [11,12].
Содержанием идентификационных измерений является измерение формы и вариабельности сигналов. Под понятием «форма» понимается вид распределения мгновенных значений (РМЗ) выборочной реализации сигнала. Понятие вариабельности учитывает характер распределения значений временных интервалов (РВИ) сигнала, формируемых при пересечении сигналом некоторого, например нулевого, уровня.
Основная идея вышеупомянутых работ состоит в том, что различные проявления свойств сигналов, описываемых понятиями формы и вариабельности, могут быть выражены количественно, в виде особых, идентификационных чисел. Идентификационные числа (параметры) обладают свойствами масштабной инвариантности, идентификационной эквивалентности и согласованной упорядоченности. Для теории измерений такой подход позволил обнаружить, ранее неизвестные, закономерности, связывающие между собой различные формы сигналов. Количественные соотношения между распределениями мгновенных значений сигналов разной формы получили название идентификационных шкал (ИШ). Примером ИШ может служить таблица 1, в которой имена распределений случайных сигналов оцифрованы с помощью, так называемого, S-тестера [13].
При этом, для обозначения случайных сигналов были использованы сокращения, принадлежащие словарю имен симметричных распределений: двумодального (2mod), арксинусного (asin), равномерного (even), треугольного (simp), нормального (gaus), двустороннего экспоненциального (lapl) и Коши (kosh).
Таблица 1
Идентификационная характеристика S-тестера
|
IdP=S N=10000,L=100 |
Вид распределения случайного сигнала |
||||||
|
2mod |
asin |
even |
simp |
gaus |
lapl |
kosh |
|
|
Rank |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Mean (S), |
1 |
0,923 |
0,75 |
0,51 |
0,317 |
0,153 |
0 |
|
Error (p=0,95),% |
0 |
0,56 |
1,07 |
2,08 |
9,5 |
18,3 |
167 |
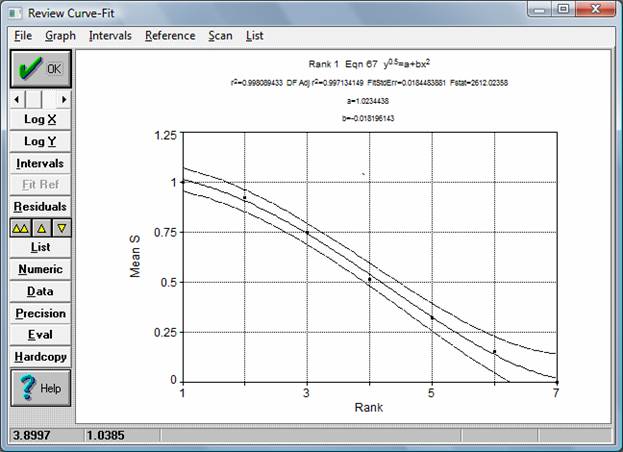
Рис. 1. Представление ИШ в виде ранговой зависимости.
Регулярный характер ИШ служит основой для ее аналитического описания (рис. 1), что, в свою очередь, позволяет вести интерполяцию положения измеряемого распределения между оцифрованными отметками шкалы.
Хотя в настоящее время в области ИИ создан достаточный научный задел для того, чтобы перейти на уровень конкретных технических решений, развитие собственно теории ИИ наталкивается на нерешенность одной важной проблемы. Эта проблема связана с отсутствием описания базовой модели сигнала, выраженной в определенной системе идентификационных параметров.
Целью данной работы является разработка идентификационной модели сигналов, а также физическая интерпретация основных параметров этой модели, которая учитывает характер (случайный, периодический ) сигнала и форму распределения его мгновенных значений.
ОСНОВЫ ТЕОРИИ
Для удобства понимания задачи, рассмотрим наиболее простую классическую модель сигнала, как вектора, вращающегося в комплексной плоскости [14]. Длина вектора определяется действующим значением сигнала. Исходное положение вектора задается начальной фазой сигнала, а скорость вращения – циклической (круговой) частотой. Для дальнейшего анализа достаточно взять временную зависимость одной из проекций вектора сигнала, например, на мнимую ось:
, (1)
где: Xm – амплитуда, θ – начальная фаза, ω – круговая частота, t – время, являющееся в (1) независимой переменной. Остальные величины (Xm , θ и ω) называются параметрами сигнала, из которых только параметр (ω) скорости вращения является составным:
,
(2)
определяемым произведением некоего коэффициента (2π) на линейную частоту (F). Поскольку линейная частота измеряется в герцах (Гц) или в 1/с, а коэффициент (2π) интерпретируется как угол, на который поворачивается вектор сигнала за время t = T = 1/F и измеряется, соответственно, в радианах, то угловая частота (ω) имеет размерность рад/с.
Хотя формула (1) называется аналитической моделью сигнала X(t), она содержит очень важный лингвистический компонент, представленный термом «SIN», явно указывающим на такую форму сигнала, для которой справедливо, в частности, и соотношение (2).
Исходя из этого, введем первое обобщение формулы (2), как соотношения, связывающего численные оценки частоты (F) и формы (А):
.
(3)
Физический смысл обобщения (3) состоит в том, что оно постулирует зависимость угловой скорости вращения вектора не только от частоты, но и от формы сигнала. В частности, векторы двух сигналов прямоугольной и синусоидальной формы, имеющие одинаковую частоту, будут вращаться с разной скоростью. Размерность коэффициента А, назовем его параметром формы, получается естественным образом, как [A] = [ω]/[F] = [радиан].
Второе, предлагаемое обобщение связано с записью математической модели вектора сигнала, по аналогии с формулой (1), как:
,
(4)
где: лингвистический терм «FRM» обозначает некое, стандартизированное имя сигнала (как, например, SIN – для синусоидального сигнала). При этом, между именем (FRM, сокращение от FORM) сигнала и численной оценкой (Afrm) его формы существует логическая, а не аналитическая (т.е. задаваемая формулой) связь.
Познавательное значение модели (4) состоит в том, что она, во-первых, в явном виде указывает на те, дополнительные (кроме Xm, F и θ) параметры (FRM, Afrm), какие надо знать, чтобы полностью описать сигнал. Во-вторых, с помощью этой модели объединяются процедуры идентификации и измерения. В-третьих, степень предлагаемого обобщения модели (4) такова, что позволяет описать не только все множество периодических сигналов сложной (не только синусоидальной) формы, но и случайные сигналы с произвольной формой распределения вероятностей, о чем будет сказано ниже. В-четвертых, изменяется физическая интерпретация частоты F. В-пятых, модель (4) позволяет сформировать алгоритм измерения формы сигналов.
Для решения последней задачи запишем уравнение (4) относительно параметра формы (Afrm), полагая, что сигнал наблюдается за время, равное периоду T0, а начальная фаза равна 0 (θ = 0). Тогда, имеет место равенство:
,
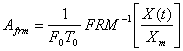(5)
где: FRM-1 – имя функции, обратной к FRM. Например, если FRM = SIN, то FRM-1 = ASIN. При измерении, значения (Afrm) усредняются за период, поэтому интегральное значение параметра формы будет определяться формулой 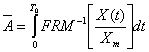(6):
.
(6)
При выводе этой формулы учтено, что произведение F0 * T0 = 1. Поскольку на практике преимущественно используются цифровые методы измерения, источником информации для которых служат дискретные выборочные реализации сигналов, то, в этом случае, оценку параметра формы следует проводить, используя формулу 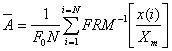(7):
, (7)
где: x(i) – значение i-го отсчета дискретной выборки, N – объем выборки. Зная частоту F0, амплитуду Xm и имя FRM формы сигнала, можно оценить числовое значение параметра формы А и сопоставить между собой пару A – FRM, образовав, тем самым, идентификационное соотношение.
Однако, сложность состоит в том, что, чаще всего, A и FRM являются априорно неизвестными величинами. Поэтому необходимо найти какой-нибудь путь независимого определения, либо значения A, либо имени FRM сигнала по той же выборке. Для этого, воспользуемся результатами работы [15], в которой на основе анализа фрактальной модели роста популяции (модель Ферхюльста [16]), была предложена формула непосредственного оценивания значения круговой частоты ω в виде:
.
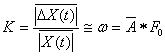(8)
В нее входят следующие параметры: 
- среднее значение модуля
приращений сигнала X(t), 
- среднее значение модуля
сигнала. Если известна аналитическая форма записи входного сигнала X(t), то можно получить (точно или приближенно) формулу для
расчета параметра K. Так, например, для синусоидального сигнала, модель которого представлена формулой (1), параметр К равен круговой
частоте ω входного сигнала 
, где параметр Asin = 2π определяет синусоидальную форму
сигнала.
Третье обобщение связано с интерпретацией величины F, которая в классической модели имеет
смысл линейной частоты. В частности, при анализе выборочных реализаций случайных
сигналов, имеющих один и тот же закон распределения вероятностей (
),
величина F0 в (8) будет случайной величиной. Чтобы оценить
математическое ожидание этой случайной величины, по совокупности реализаций L, можно использовать, например,
формулу для среднеарифметического значения:
.
(9)
В дальнейшем, величину Fc будем называть характеристической частотой сигнала, и использовать ее в моделях (4 и 8), вместо линейной частоты F. Физический смысл понятия «характеристическая частота» состоит в том, что для периодических сигналов ее значение совпадает с реальной, физической частотой. Для случайных сигналов, характеристическая частота является оценкой частоты появления экстремальных значений за время наблюдения. Только для постоянных во времени сигналов характеристическая частота равна 0.
Формула (8) удобна еще и тем, что содержит информацию об амплитуде сигнала в виде средневыпрямленного значения. В свою очередь, амплитудное и средневыпрямленное значения связаны с формой сигнала [17], что в общем виде может быть выражено соотношением:
. (10)
Таким образом, чтобы полностью определить идентификационную модель (4) сигнала (при θ=0), необходимо:
1)Анализировать не только сам сигнал X(t), но и его приращения ΔX(t).
2)Измерить средневыпрямленное значение
сигнала
и использовать
его как оценку амплитуды (10).
3)Измерить средневыпрямленное значение
приращений сигнала и по формуле (8) оценить параметр K (круговую частоту ω).
4) Отделить параметр формы 
от характеристической частоты Fc в (8), для чего:
· упорядочить (отсортировать) выборочную реализацию сигнала X(t), например, по возрастанию U = Sort [X(t)];
·
по формуле (8)
оценить параметр K = Ks для сортированной функции U, при этом определится параметр формы (), так как для сортированной функции
сигнала значение круговой частоты (Ks) от характеристической частоты не
зависит (Fc = 1);
· оценить отношение круговых частот для несортированной и сортированной функций
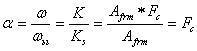, (11)
которое будет равно характеристической частоте.
5)Установить логическое соответствие для
пары 
, используя идентификационную
шкалу (ИШ) сигналов.
6)Записать уравнение идентификационной модели сигнала в виде (4), подставив в нее числовые и лингвистические значения параметров.
В представленном алгоритме построения идентификационной модели сигналов присутствует очень важная процедура 5), выполнение которой требует использования ИШ сигналов.
В отличие от ИШ
S-типа (табл. 1, рис. 1), в данном
случае предлагается использовать шкалу FRaSH-типа [18], которая состоит из двух компонент:и 
(табл. 2).
Таблица 2
Идентификационная шкала распределений симметричных
случайных сигналов
|
N=10000, L=100 |
Вид распределения случайного сигнала |
||||||
|
2mod |
asin |
even |
simp |
gaus |
lapl |
\kosh |
|
|
Rank |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Afrm |
4 |
6,28 |
8 |
12 |
19 |
36 |
3000 |
|
Fc |
2500 |
2027 |
1667 |
1180 |
736 |
416 |
6 |
|
Аналог |
squ |
sin, cos |
tri, saw |
|
|
|
|
Численные оценки идентификационных параметров Afrm , Fc получены усреднением 100 выборочных реализаций случайных сигналов, объема N = 10000. В строке «Аналог» указаны имена периодических сигналов прямоугольной (squ), синусоидальной (sin), косинусоидальной (cos), треугольной (tri) и пилообразной формы, имеющих такие же значения параметра формы, как и у случайных сигналов с двумодальным (A2mod = Asqu),арксинусным (Aasin = Asin = Acos) и равномерным (Aeven = Atri = Asaw) распределениями.
На рис 2. представлены ранговые (порядковые) зависимости формы и характеристической частоты случайных сигналов.
Условие, при котором два разных сигнала имеют одинаковую оценку параметра формы, будем называть идентификационной эквивалентностью. На рис. 3 показан пример идентификационного моделирования периодического и случайного сигналов, имеющих одинаковое (asin) распределение мгновенных значений и, следовательно, эквивалентных в отношении РМЗ.
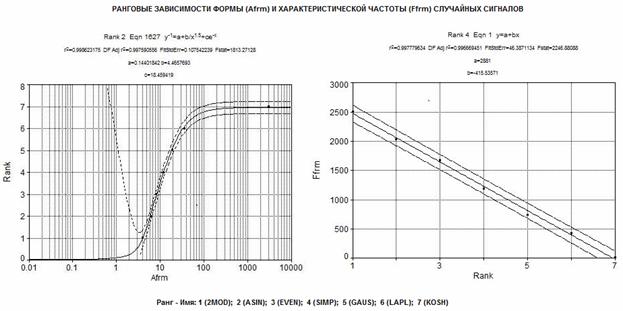
Рис. 2. Ранговые зависимости формы и характеристической частоты случайных сигналов.
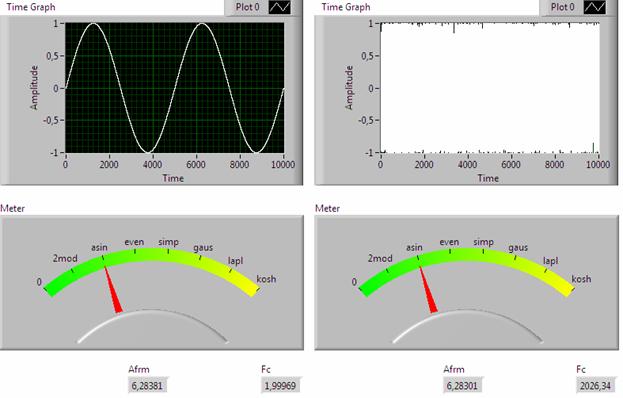
Рис. 3. Пример идентификационного моделирования периодического (слева) и случайного сигналов, имеющих одинаковое (asin) распределение.
Идентификационные модели рассмотренных в данном примере сигналов, с учетом объема выборки (N = 10000) и использования словаря имен периодических сигналов, могут быть записаны следующим образом:
Xper(t) = 0,64*0,5 π *SIN(2π*2t) = SIN(2π*0,0002t), t = 0..N,
Xrnd(t) = 0,64*0,5 π *SIN(2π*2027t) = SIN(2π*0,2027t), t=N*RND,
где: RND – равномерно распределенная в диапазоне 0..1 случайная величина.
Следовательно, эти два сигнала эквивалентны в отношении амплитуды и формы, но отличаются, во-первых, по значению характеристической частоты и, во-вторых, по общему виду зависимости X(t). Чтобы увеличить степень общности сигналов в отношении эквивалентности, мысленно сделаем частоту периодического сигнала, равной характеристической частоте случайного.
Эквивалентность сигналов, наступающая при равенстве характеристических частот, может служить критерием разделения классов периодических и случайных сигналов. С учетом того, что реальные сигналы представлены своими выборочными реализациями, принадлежность сигнала, либо к классу периодических, либо к классу случайных, можно записать в виде условия:
IF Ω = Afrm*Fc ≥ N THEN X(t) = Xrnd(t) ELSE X(t) = Xper(t) ,
где: N – объем выборочной реализации сигнала. Данный критерий (Ω) имеет физический смысл круговой частоты, при которой периодический сигнал выглядит как случайный. При этом можно оценить такой важный параметр дискретизированного сигнала, как разрешающая способность: R = N/ Fc , которая для рассматриваемого примера составляет R= 10000/2027 ≈ 5 отсчетов на период сигнала.
Учитывая вышеизложенное, обобщенная идентификационная модель сигналов может быть формально представлена через физические параметры как:
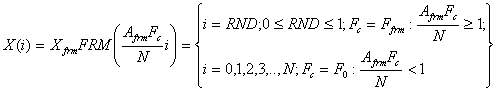, (12)
где: RND – равномерно распределенная случайная величина; Ffrm - характеристическая частота Fc случайного сигнала, зависящая от формы его распределения (табл. 2); F0 - характеристическая частота Fc периодического сигнала, определяемая его источником.
Из (12) следует, что, во-первых, случайные и периодические сигналы отличаются областями определения. Во-вторых, эти классы сигналов имеют различные по физическому смыслу независимые переменные, задающие условное время: 0≤RND≤1 (для случайного сигнала) и 0≤i≤N (для периодических сигналов). В-третьих, случайные сигналы имеют постоянное значение характеристической частоты (Ffrm) для заданной формы распределения, в то время, как частота периодического сигнала (F) определяется источником этого сигнала. При этом, все случайные сигналы, образующие ИШ (табл. 2), не являются независимыми, а связаны - нелинейно по форме, но линейно по характеристической частоте (рис. 2).
Чтобы иметь возможность отличать случайные сигналы от периодических, по формальной записи модели (12), примем следующее правило:
IF X(t) = RND THEN FRM = DName [X(t)] ELSE FRM = DName(-1) [X(t)].
Другими словами, если сигнал случайный, то лингвистический терм FRM получает имя распределения (DName [X(t)]) из соответствующего набора имен оцифрованных отметок ИШ (табл. 2). Поскольку словарь имен периодических сигналов весьма ограничен, а самих сигналов может быть множество, то для обозначения периодического сигнала используется имя распределения случайного сигнала, которое дополняется меткой (-1), обозначающей имя, обратное к имени распределения.
В качестве примера, на рис. 4 показаны формальные записи сигналов, изображенных на рис. 3. В этих записях указаны также области определения независимых переменных и классификационные признаки (PER, RND) сигналов.
Рис. 4. Примеры формальной записи идентификационных моделей периодического (вверху) и случайного (внизу) сигналов.
МЕТОДИКА И ИНСТРУМЕНТЫ ИССЛЕДОВАНИЯ
Для экспериментальной проверки правильности теоретических положений, сформулированных в предыдущем разделе, был разработан в среде LabVIEW-7.1 виртуальный прибор (ВП), структурная схема которого показана на рис. 5. Данный ВП содержит: универсальный генератор (UniGen) сигналов; блок идентификационных измерений (Identification Block); блок усреднения (Mean) и блок синтеза модели (Model Synthesis Block). Выходная информация представляет собой запись, аналогичную формуле (12) и содержащую в правой части следующие компоненты: оценку амплитуды сигнала (по формуле (10)); имя (FRM) формы распределения; оценку параметра формы Afrm; оценку характеристической частоты (Fc); объем (N) выборки (через правый бэкслэш); обозначение независимой переменной (i – для периодических и RND – для случайных сигналов); область определения независимой переменной и классификационный (PER, RND) признак сигнала.
В цикле For-Next генератор формирует L – реализаций сигнала, объема N. Блок идентификационных измерений оценивает параметры сигналов. В устройстве Mean происходит усреднение измеренных значений параметров по числу реализаций. В блоке синтеза модели по усредненным оценкам идентификационных параметров проводится логический анализ и формирование выходного суждения в виде записи уравнения модели. В левой нижней части рис. 5 даны примеры записей 7-ми разновидностей случайных сигналов и 3-х разновидностей – периодических. В правой нижней части помещен пример анализа случайного сигнала с экспоненциальным распределением, имя которого отсутствует в ИШ (табл.2).
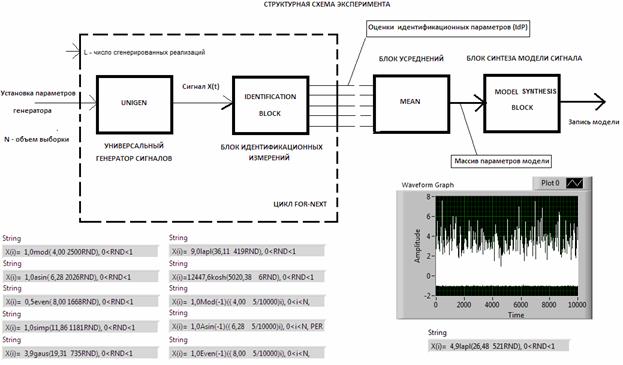
Рис. 5. Структурная схема ВП и примеры его работы.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ
Целью экспериментальных исследований являлось выяснение особенностей реакции системы моделирования (рис. 5) на различные типы сигналов. При этом, логический модуль системы настраивался на распознавание только двух классов сигналов: симметричных случайных и периодических. Для этих сигналов выходные записи полностью соответствовали генерируемым выборкам, что подтверждается результатами моделирования, помещенным на рис. 5.
Первая особенность связана с зависимостью вида модели от постоянной составляющей входного сигнала.
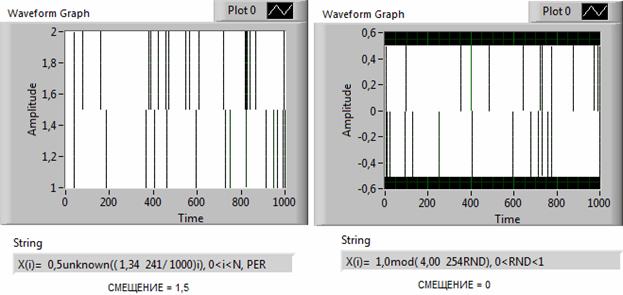
Рис. 6. Пример влияния смещения сигнала на вид модели.
В частности, показанный на рис. 6, пример иллюстрирует факт качественных отличий в записях моделей одного и того же случайного сигнала с двумодальным распределением. Сигнал на левом графике имеет смещение и классифицируется как неизвестный, периодический. У сигнала на правом графике смещение отсутствует, и он классифицирован правильно – как случайный сигнал. Причиной данного эффекта является зависимость средневыпрямленного значения сигнала от постоянной составляющей, что, в свою очередь, непосредственно влияет (по формуле (8)) на значение оценок параметра формы и характеристической частоты. Устранить причину неадекватности достаточно просто. В обоих случаях, это достигается включением на входе блока идентификационных измерений, либо специального компенсационного модуля (при реализации на программном уровне), либо разделительных конденсаторов (при реализации на аппаратном уровне).
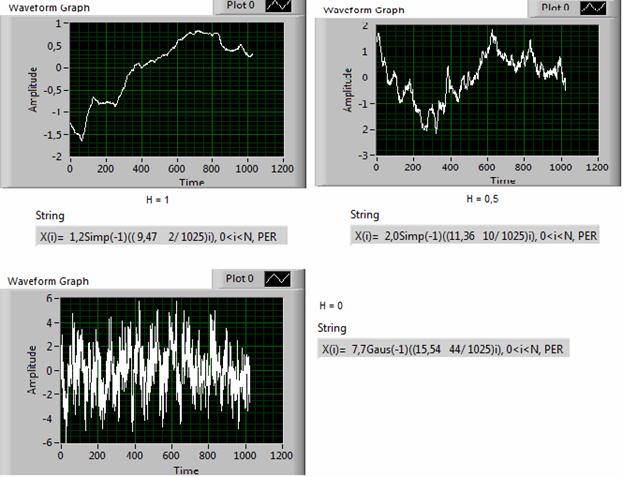
Рис. 7. Примеры фрактальных сигналов с разными значениями показателя Херста (Н=1, Н=0,5, Н=0).
Вторая особенность, проявляющаяся в неадекватном отображении входного сигнала его моделью, связана с внутренней структурой некоторых типов сигналов. Наиболее отчетливо это видно на примере моделей фрактальных сигналов (рис. 7), показатель Херста которых изменяется в диапазоне от 0 до 1. Хотя все эти сигналы выглядят, как случайные, системой они идентифицируются, как периодические. Аналогичный эффект наблюдается для музыкальных и некоторых случайных сигналов (рис. 8). Можно предположить, что такое поведение системы связано с ее способностью выявлять наличие явных или латентных трендов и периодичностей.
Третья особенность вытекает из сравнения моделей сигналов, представленных на рис. 8. Эти сигналы имеют общую область определения (0≤i≤N) и одинаковый классификационный признак (PER), причисляющий их к группе периодических сигналов.
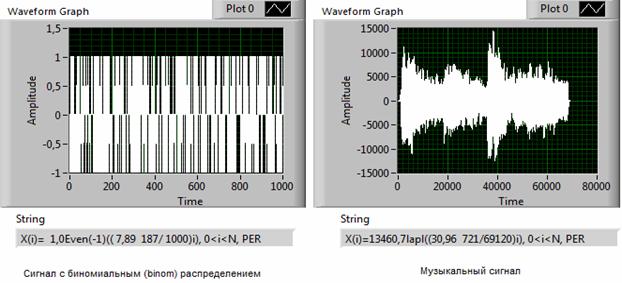
Рис. 8. Примеры сигналов, содержащих скрытые периодичности.
Отличие проявляется в разных типах словарей имен, служащих для обозначения лингвистического терма FRM. В частности, для обозначения случайного сигнала с биномиальным распределением использован словарь имен периодических сигналов (Even(-1)), а для музыкального сигнала – словарь имен случайных сигналов (lapl). Это обстоятельство указывает на существенную разницу, заметную даже визуально, в структуре сигналов. Поэтому, деление сигналов только на 2 группы: периодических и случайных, является явно не достаточным.
ВЫВОДЫ И РЕКОМЕНДАЦИИ
В связи с новыми знаниями о моделях сигналов, полученных на основе развития теории идентификационных измерений, принятые в современной теории сигналов классификационные построения нуждаются в существенном уточнении и, в некоторых случаях, переработке. Наши предложения сводятся к следующему.
Во-первых, вместо понятий «случайный сигнал» и «периодический сигнал» использовать, более широкие по смыслу, понятия «хаотический сигнал» и «регулярный сигнал». Это связано с тем, что понятие регулярности включает в себя понятия, описывающие, как периодические сигналы, так и сигналы, имеющие тренды. Количественным показателем степени регулярности-хаотичности следует считать численную оценку угловой скорости вращения (8) идентификационного вектора сигнала (0≤K≤2). При K = 0, имеем «абсолютно регулярный сигнал», примером которого может служить сигнал X(-∞<t<+∞) = const, а при K = 2 – «абсолютно хаотичный», примером которого может служить случайный сигнал, имеющий плотность вероятности в виде δ-функции. Если K =1, это означает, что весовое соотношение между регулярностью и хаотичностью равно 50% (сигнал одновременно и «не регулярный», и «не хаотический»). В качестве модели такого представления сигналов, может быть использована, например, принадлежностная (нечеткая [19]) идентификационная шкала типа:
,
(13)
где: µ(K) – функция принадлежности.
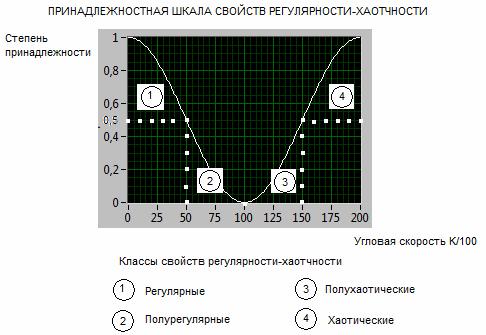
Рис. 9. Принадлежностная идентификационная шкала свойств регулярности-хаотичности.
В этом случае, естественно делить сигналы по вариабельности не на два, а на четыре, класса (рис. 9).
Границы раздела классов не обязательно должны быть результатом равномерного разбиения диапазонов. Вполне допустимы границы, назначенные соглашением экспертов и учитывающие специфику некоторой предметной области. Например, можно установить границы, ограничивающие области 2 и 3 (рис.9) и расширяющие, соответственно области 1 и 4. Интересен также вариант введения пятого класса, как переходного между областями 2 и 3. В этом случае удается ввести количественную оценку понятия «неопределенность», как такого свойства сигнала, при котором степень его принадлежности понятиям «регулярность» и «хаотичность» равна нулю. Примерами таких, «неопределенных» сигналов служат сигналы, изображенные на рис.10. Хотя данные сигналы входят в один и тот же нулевой (null) класс вариабельности, они имеют разные параметры амплитуды, формы, характеристической частоты и разрешения.
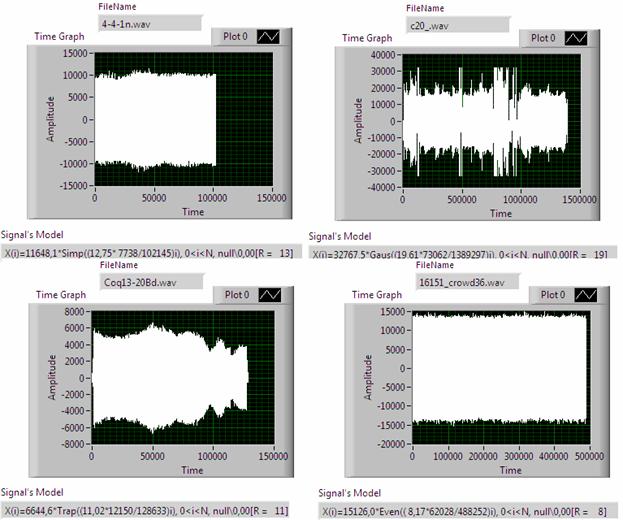
Рис. 10. Примеры сигналов, имеющих нулевую степень принадлежности по шкале вариабельности (рис. 9).
Во-вторых, идентификационные шкалы формы (табл. 2) и вариабельности (13) являются круговыми. Это означает, что начальная и конечная точки ИШ совпадают. Данная особенность является следствием «фазового» происхождения идентификационных параметров, определяющих форму и характеристическую частоту сигналов. Отсюда следует, что все непрерывное множество известных и еще неизвестных типов сигналов уже находится внутри этих шкал. В качестве аналогии можно привести пример таблицы химических элементов (ТХЭ) Д.И. Менделеева. Поскольку ТХЭ является объективной классификацией, вмещающей все множество открытых и неизвестных элементов, то и классификация сигналов, построенная по принципу (13) идентификационных измерений, может служить основой создания новых, объективных классификационных систем сигналов.
В-третьих, свойство эквивалентности регулярных и хаотических сигналов по моделям (12,13) указывает на то, что известную задачу цифровой обработки по дискретизации сигналов, необходимо решать с учетом формы сигналов. При этом справедлива следующая закономерность: чем сложнее форма сигнала, тем больше (по сравнению с теоремой Котельникова) должно быть соотношение между частотой сигнала и частотой дискретизации. В частности, проведенные расчеты разрешающей способности показывают, что для синусоидального сигнала частота дискретизации должна примерно в 5-6 раз превышать его физическую частоту. При данных условиях, сигнал может быть восстановлен с требуемой точностью полиномом первой степени. К подобному же выводу эмпирическим путем пришли разработчики цифровых сверхвысокочастотных осциллографов известной фирмы TEKTRONIX [20].
ЛИТЕРАТУРА
1. Кликушин Ю.Н. Представление случайных сигналов с помощью принадлежностных спектров// Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 2 (февраль), 2000 г. http://jre.cplire.ru/jre/feb00/4/text.html
2. Кликушин Ю.Н. Фрактальная шкала для измерения распределений вероятности// Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 3 (март), 2000 г. http://jre.cplire.ru/jre/mar00/2/text.html
3. Кликушин Ю.Н. Метод фрактальной классификации сложных сигналов// Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 4 (апрель), 2000 г. http://jre.cplire.ru/jre/apr00/1/text.html
4. Кликушин Ю.Н. Классификационные шкалы для распределений вероятности// Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 11 (ноябрь), 2000 г. http://jre.cplire.ru/jre/nov00/4/text.html
5. Кликушин Ю.Н. Количественная оценка свойств "регулярности-хаотичности" сигналов// Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 10 (октябрь), 2006 г. http://jre.cplire.ru/jre/oct06/1/text.html
6. Кликушин Ю.Н., Кобенко В.Ю. Основы идентификационных измерений// Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 11 (ноябрь), 2006 г. http://jre.cplire.ru/jre/nov06/2/text.html
7. Кликушин Ю.Н., Кошеков К.Т. Классификатор сигналов// Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 10 (октябрь), 2007 г. http://jre.cplire.ru/jre/oct07/3/text.html
8. Кликушин Ю.Н. RGB-шкала для измерения распределений// Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 3 (март), 2008 г. http://jre.cplire.ru/jre/mar08/3/text.html
9. Кликушин Ю.Н. Идентификационный метод цифровой обработки сигналов// Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 5 (май), 2010 г. http://jre.cplire.ru/jre/may10/5/text.html
10. Кликушин Ю.Н., Кошекова Б.В. Идентификационный алгоритм децимации сигналов// Интернет-статья, М.: Журнал Радиоэлектроники, ИРЭ РАН, № 6 (июнь), 2010 г. http://jre.cplire.ru/jre/jun10/1/text.html
11. Кликушин Ю.Н. Технологии идентификационных шкал в задаче распознавания сигналов: монография / Ю.Н. Кликушин. - Омск: Изд-во ОмГТУ, 2006. - 96 с.
12. Кликушин Ю.Н., Кошеков К.Т. Методы и средства идентификационных измерений сигналов: монография / Ю.Н. Кликушин, К.Т. Кошеков. – Петропавловск: Изд-во СКГУ им. М. Козыбаева, 2007. – 186 с.
13. Кликушин Ю.Н., Кошеков К.Т., Кошекова Б.В. Транслятор как универсальный инструмент идентификационных измерений.//Информационно-измерительные и управляющие системы. - М.: Радиотехника, №9, т.6, 2008. с.24-30.
14. Гоноровский И.С. Радиотехнические цепи и сигналы. – М.: Советское радио, 1977.
15. Кликушин Ю.Н., Кошеков К.Т. Модель роста популяции в задаче автоматической классификации сигналов // Омский Научный Вестник – Омск: Изд-во ОмГТУ, №4(33), 2005, с.160-163.
16. Пайтген Х.-О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем: Пер. с англ. – М.: Мир, 1993. - 176 с.
17. Измерения в электронике // Справочник. Под ред. В.А.Кузнецова. - М.: Энергоатомиздат, 1987. - 511 с.
18. Кликушин Ю.Н. Идентификационные инструменты анализа и синтеза формы сигналов: монография / Ю.Н. Кликушин. – Омск: Изд-во ОмГТУ, 2010. – 216 с.
19. Нечеткие множества в моделях управления и искусственного интеллекта // Под ред. Д.А.Поспелова. – М.: Наука,1986.