| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 4, 2001 |
ПРОСТРАНСТВЕННОЕ КОДИРОВАНИЕ ИНФОРМАЦИИ В ЗАДАЧЕ РАСПОЗНАВАНИЯ ОБЪЕМНЫХ ОБЪЕКТОВ
В. И. Шанин, О. В. Шанин
МАТИ - Российский Государственный технологический университет им. К.Э. Циолковского
Получена 28 мая 2001 г.
В статье рассмотрены возможности метода пространственного кодирования информации с помощью решетчатых структур для решения задач распознавания объемных объектов. Здесь представлены результаты теоретических и экспериментальных исследований процессов кодирования и обработки информации применительно к этому, точностных возможностей метода, установлены требования к позиционированию объектов на входе систем распознавания, а также приведены варианты схемных решений при построении датчиков структурного освещения и систем распознавания как с электронной, так и с оптической обработкой информации.
Получены
аналитические выражения для описания процесса кодирования и поведения
корреляционного отклика от изменения формы распознаваемого объекта и его
положения на входе системы распознавания. Установлено, что относительная
точность распознавания объемных объектов находится в пределах 10![]() -10
-10![]() . Для
повышения точности предложено использовать дискретизацию входной информации.
Результаты экспериментальных исследований достаточно хорошо согласуются с
данными теоретического анализа.
. Для
повышения точности предложено использовать дискретизацию входной информации.
Результаты экспериментальных исследований достаточно хорошо согласуются с
данными теоретического анализа.
Введение
1. Математическая модель кодирования с помощью
решетчатых структур
2. Математическая
модель процесса распознавания
3. Исследование метрологических возможностей метода
4. Требования к точности позиционирования объектов
5. Ограничения метода
6. Экспериментальные исследования метода
7. Принципы построения систем
распознавания на базе пространственного
кодирования информации
Внимание к методам пространственного кодирования информации обусловлено проблемой распознавания образов, а именно распознаванием трехмерных объектов [1, 2] и анализом объемных сцен по их изображениям [3]. Сложность решения этой проблемы связана, с одной стороны, с необходимостью переработки большого объема информации (для выделения основных признаков распознаваемых образов), а с другой стороны, - с недостаточной информативностью изображений трехмерных объектов. Поэтому в проблеме распознавания трехмерных образов к настоящему времени наметились два направления.
Первое направление связано с применением методов обработки информации, имеющей избыточную информативность, и оно сводится к отфильтровыванию малоинформативных составляющих [4]. Второе направление относится к ситуации, когда, наоборот, изображения обладают недостаточной информативностью, например, при высоком уровне шумов или если изображения распознаваемых образов близки между собой [3].
Известные методы пространственного кодирования информации основаны на создании вспомогательных сигналов на поверхности объемных тел, которые либо слабо связаны со свойствами распознаваемых объектов, либо вообще не связаны с ними [5].
Применительно к задачам контроля и дефектоскопии промышленной продукции, которые являются разновидностью проблемы распознавания образов, наибольшего внимания заслуживают методы пространственного кодирования информации с помощью решетчатых структур [2].
Суть этих методов состоит в получении плоского изображения, являющегося топографической картой (топограммой) поверхности исследуемого объекта. Линии на такой топограмме, называемые линиями равного уровня, - это следы сечения поверхности объекта равностоящими друг от друга плоскостями. В результате топограмма несет в себе информацию как о конфигурации изделия, так и о рельефе его поверхности. Трансформация структуры кодирующего сигнала на изображении распознаваемого объекта, обусловленная особенностями его формы, обеспечивает высокую информативность изображения при градационной его простоте - две градации (светлое и темное).
В настоящее время известны два метода пространственного кодирования информации:
- кодирование с помощью решетчатых структур [6],
- кодирование с помощью голографической интерферометрии [7,8].
В работах [6, 9] показаны перспективы применения пространственного кодирования с помощью решетчатых структур для промышленного контроля и дефектоскопии изделий со сложной формой поверхности.
Однако широкое внедрение систем распознавания на базе пространственного кодирования в практику сдерживается рядом нерешенных технических вопросов. К таким вопросам относятся метрологические возможности таких систем, требования к точности позиционирования объектов, выбор и требования к элементной базе, а также принципы построения систем распознавания с учетом особенностей обработки полученной информации. Рассмотрению перечисленных вопросов и посвящена настоящая работа.
Ниже рассматриваются математические модели процессов кодирования и анализа объектов со сложной формой поверхности в системах с корреляционной обработкой информации, теоретическая оценка метрологических возможностей таких систем и требования к позиционированию объектов на их входе, а также экспериментальные данные, варианты структурных схем систем распознавания и особенности выбора и топологии элементов в этих системах.
1. Математическая модель кодирования с помощью решетчатых структур
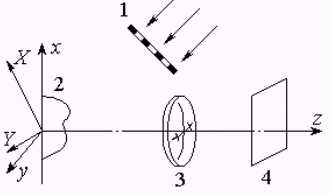
Принципы кодирования пространственной информации с помощью решетчатых структур поясним рис.1. Его суть состоит в пространственной модуляции плоской световой волны, освещающей объемное тело, регулярной двумерной структурой (решеткой). При этом на поверхности объемного тела формируется контрастный узор, вид которого однозначно связан с кривизной поверхности объекта, углом, под которым он освещается, и ракурсом его наблюдения. Основная особенность пространственного кодирования заключается в том, что исходная информация о форме объекта имеет вид простого по градациям (регулярных темных и светлых участков) изображения. Отсюда, как следствие, существенно снижаются требования к динамическому диапазону приемных светочувствительных приборов. Главное же достоинство такой формы представления информации состоит в ее хорошем соответствии возможностям устройствами оптической согласованной фильтрации для дальнейшего анализа [10].
Сказанное математически можно пояснить следующим образом. Любой трехмерный объект в пространстве характеризуется как поверхность
Пусть этот объект наблюдается в направлении оси OZ (рис. 2). Тогда в нем можно выделить контурную и рельефную части. Контур объекта, наблюдаемого в направлении оси OZ, определим как проекцию поверхности O(x, у, z) на плоскость P, перпендикулярную к оси OZ. Обозначим его в виде функции C(x0, у0), которая представляет собой замкнутую линию в плоскости P. При этом положим, что
![]()
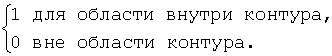
Рельеф объекта представим как функцию высоты Z точки M поверхности O(x, у, z) и обозначим как f (x, y), т. е. запишем
Рис. 1. Схема пространственного кодирования информации с помощью регулярной двумерной структуры, где: 1 - решетка, 2 - трехмерный объект, 3 - оптическая система, 4 - плоскость регистрации изображения.
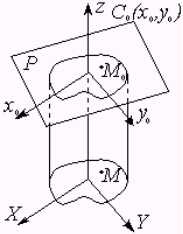
Рис. 2. Геометрическое представление
трехмерного объекта как функций контура C(x,
y) и рельефа ![]() , описывающегося через высоту
Z точек M поверхности объекта.
, описывающегося через высоту
Z точек M поверхности объекта.
При освещении объекта в соответствии с рис. 1 распределение света на выходе решетки будет иметь вид
где X — координата, связанная с системой освещения; b — ширина щели; 2b — период решетки; comb(x) — гребенчатая функция, определяемая как
![]() ,
, ![]() - функция Дирака;
- функция Дирака;
rect(x) — прямоугольная функция, определяемая как
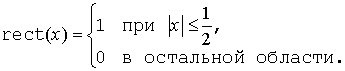
Поскольку система координат освещения (X, Y, Z) cвязана с системой координат наблюдения (x, y, z) соотношением
то выражение (3) можно записать как
Если теперь в плоскость наблюдения поместить оптический носитель информации, то его амплитудное пропускание будет описываться выражением
где
![]() — система координат в плоскости носителя
информации,
— система координат в плоскости носителя
информации, ![]() — освещенность объекта без кодирования.
— освещенность объекта без кодирования.
Для упрощения дальнейших рассуждений примем
![]() ,
,
![]() .
.
Кроме того, положим, что освещенность E однородна внутри контура и равна 1, а также отметим [6], что
где
N — число щелей в решетке, ![]() — коэффициенты ряда Фурье.
— коэффициенты ряда Фурье.
Подставив (7) в (6), окончательно получим
Из анализа выражения (8) видно, что изображение на транспаранте содержит в себе информацию как о контуре, так и о рельефе исследуемого трехмерного объекта.
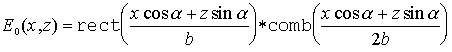 . (5)
. (5)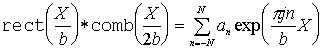 , (7)
, (7)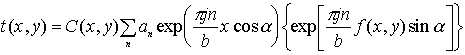 . (8)
. (8)