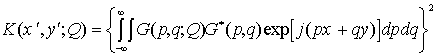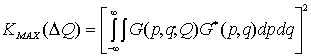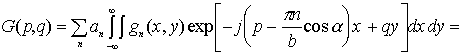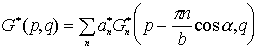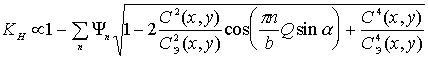2. Математическая модель процесса распознавания
Как известно [4], процесс распознавания состоит в нахождении функции взаимной корреляции эталонного и распознаваемого образов. В зависимости от физического характера информации эта операция достаточно успешно решается с помощью либо электронных [11], либо когерентно-оптических средств обработки информации [10]. При использовании последних функция взаимной корреляции имеет вид яркого светового пятна — корреляционного отклика, распределение интенсивности света в котором математически описывается выражением
где x,y и x¢,y¢ — координаты
входной и выходной плоскости системы обработки информации;
t и 
— амплитудное
пропускание транспарантов с изображением распознаваемого и эталонного образов; * — операция
корреляции.
Применительно к когерентно-оптическим системам обработки информации функция взаимной корреляции обычно находится через пространственные спектры распознаваемых образов в виде
где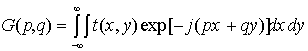 
— Фурье-спектр
распознаваемого образа с пропусканием t(x, y);
— Фурье-спектр
эталонного образа с пропусканием t(x,y);
Q — отличие между
распознаваемыми образам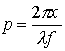и; 
и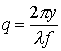 
— пространственные
частоты; 
— длина волны
света; f — фокусное расстояние линзы для
Фурье-преобразования.
Выражение для максимума функции взаимной корреляции получается из (10) при x¢ = 0 и y¢ = 0, что соответствует физическим условиям его оценки:
Итак, для получения зависимости поведения максимума корреляционного отклика необходимо иметь пространственные спектры амплитудного пропускания транспарантов изображений распознаваемых объектов. С учетом выражения (8) и точностью до постоянного множителя пространственные спектры запишутся как
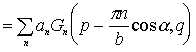и (12)
где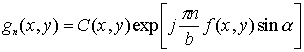 
; 
— преобразование
Фурье от функции 
.
После подстановки (12) и (13) в (11), интегрирования, необходимых преобразований и нормирования получим выражение для максимума корреляционного отклика в виде
где 
— отличие рельефа
распознаваемых объектов; индекс "э" относится к эталонному объекту; 
— функция контура
эталонного объекта; 
— функция рельефа
поверхности эталонного объекта; 
; 
— перекрестный
член.
Из анализа выражения (14) следует, что:
— если распознаваемый и эталонный объекты идентичны, т. е. 
и 
, то 
;
— если объекты имеют различия в контуре, т. е. 
и 
, то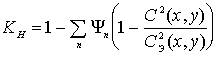 
. Видим, что корреляционный отклик содержит информацию
лишь о контурных отличиях.
— если объекты имеют одинаковые контуры, но различные рельефы поверхности,
т. е. 
и 
, то 
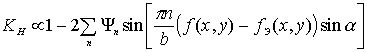. Видно, что корреляционный отклик содержит информацию
только о рельефных отличиях.